7.3 Partitions

Objectives:

•

Discover a strong connection between equivalence relations and partitions

7.3.1 A New But Familiar Construction

Example 7.3.1.

A partition of $\mathbb{Z}$ is a (finite or infinite) collection of subsets. These subsets must satisfy the following conditions:

(i)

For each $X\in\Omega$ , $X\neq\varnothing$ (i.e., each subset is nonempty).
(ii)

For all $X\neq Y\in\Omega$ , $X\cap Y=\varnothing$ (i.e., the collection of sets is pairwise disjoint, meaning that no two sets share any elements).
(iii)

$\bigcup_{X\in\Omega}X=\mathbb{Z}$ (i.e., every element of $\mathbb{Z}$ is contained within at least one subset).

Prove or disprove the following statements:

(a)

Let $A_{1}$ be the set of all odd integers and let $A_{2}$ be the set of all even integers. Then $\{A_{1},A_{2}\}$ is a partition of $\mathbb{Z}$ .

Blank space for you to write your work.
(b)

Let $A_{n}:=\{m\in\mathbb{Z}\mid m\leq n\}$ . Then $\{A_{n}\}_{n\in\mathbb{Z}}$ is a partition of $\mathbb{Z}$ .

Blank space for you to write your work.

Let us revisit the diagram from the first Example of Section 7.2. Not all of our diagrams might look the same, but perhaps we might have a diagram like this:

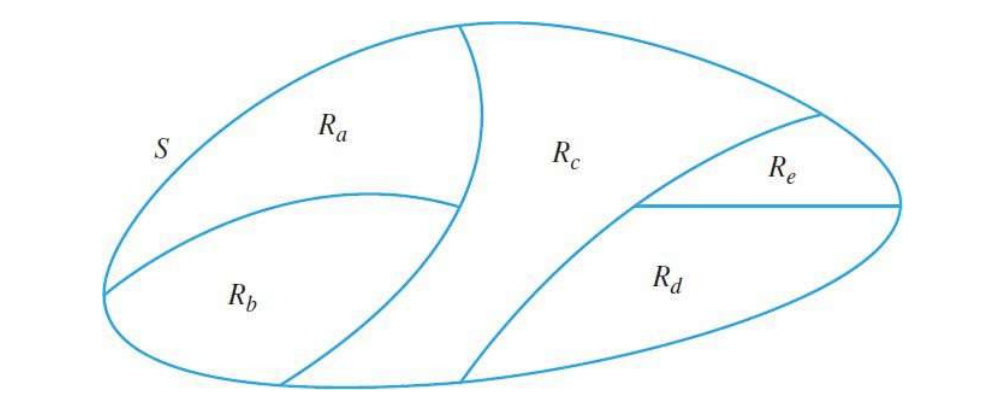
a partition of a set S into various blocks

In this diagram we noted that equivalence relations break up a set into regions. In the last example of Section 7.2 we saw that these regions satisfy a couple interesting properties. Do you see any connections between these properties and the definition of a partition?

Example 7.3.2.

Draw a diagram of a partition of $\mathbb{Z}$ . You may choose a partition from the previous example, or you may draw a different diagram. Justify that your diagram satisfies all three conditions of a partition.

7.3.2 Connecting Partitions and Equivalence Relations

Our goal in this section is to prove the statement you might be noticing from your diagram: equivalence relations and partitions are not so different from one another. Before we start proving this statement, let us investigate partitions a little further.

We begin with a formal definition, which should look very familiar to the definition we gave on the first page:

Definition 7.3.3.

Let $A$ be a set. A partition $\Omega$ of $A$ is a (finite or infinite) collection of subsets. These subsets must satisfy the following conditions:

(i)

For each $X\in\Omega$ , $X\neq\varnothing$ (i.e., each subset is nonempty).
(ii)

For all $X\neq Y\in\Omega$ , $X\cap Y=\varnothing$ (i.e., the collection of sets is pairwise disjoint, meaning that no two sets share any elements).
(iii)

$\bigcup_{X\in\Omega}X=A$ (i.e., every element of $A$ is contained within at least one subset).

We will call the subsets of $X$ blocks of the partition.

Example 7.3.4.

Find a partition of $\mathbb{Z}$ with exactly four blocks.

Example 7.3.5.

Find a partition of $\mathbb{R}$ with infinitely many blocks.

Example 7.3.6.

Consider the relation $x\sim y$ on $\mathbb{Z}$ if $4|(x-y)$ . It is given that $\sim$ is an equivalence relation. Let $[n]_{4}$ be the equivalence class of $n$ under this equivalence relation. Show that the set of equivalence classes $\{[0]_{4},[1]_{4},[2]_{4},[3]_{4}\}$ form a partition of $\mathbb{Z}$ .

Example 7.3.7.

Take your partition of $\mathbb{R}$ with infinitely many blocks. Define a relation $x\sim y$ on $\mathbb{R}$ such that $x\sim y$ if $x$ and $y$ are both in the same block of the partition. Show that $\sim$ is an equivalence relation.

In our previous two examples we saw a huge connection between our last two major concepts: “partition” and “equivalence relation”. We are now ready to prove a major connection between these two concepts:

Theorem 7.3.8.

Let $A$ be a set.

(a)

If $\sim$ is an equivalence relation on $A$ , then the set of equivalence classes $A/\sim$ form a partition on $A$ .

Blank space for you to write your work.
(b)

If $\Omega$ is a partition of $A$ , then the relation $\sim$ defined by $x\sim y$ if there exists some $X\in\Omega$ such that $x,y\in X$ is an equivalence relation.

Blank space for you to write your work.