4 Mathematical Induction

4.1 The Principle of Mathematical Induction

4.1.1 Beginning Activity 1 (Exploring Statements of the Form $(\forall n\in \mathbb{N})(P(n))$)

One of the most fundamental sets in mathematics is the set of natural numbers $\mathbb{N}$. In this section, we will learn a new proof technique, called mathematical induction, that is often used to prove statements of the form $(\forall n\in \mathbb{N})(P(n))$. In Section 4.2, we will learn how to extend this method to statements of the form $(\forall n\in T)(P(n))$, where $T$ is a certain type of subset of the integers $\mathbb{Z}$.

For each natural number $n$, let $P(n)$ be the following open sentence:

$$4\text{ divides }\left(5^n-1\right)$$

1. Does this open sentence become a true statement when $n=1$? That is, is 1 in the truth set of $P(n)$ ?

2. Does this open sentence become a true statement when $n=2$? That is, is 2 in the truth set of $P(n)$ ?

3. Choose at least four more natural numbers and determine whether the open sentence is true or false for each of your choices.

All of the examples that were used should provide evidence that the following proposition is true:

For each natural number $n,4$ divides $\left(5^n-1\right)$.

Definition. A set $T$ that is a subset of $\mathbb{Z}$ is an inductive set provided that for each integer $k$, if $k\in T$, then $k+1\in T$.

1. Carefully explain what it means to say that a subset $T$ of the integers $\mathbb{Z}$ is not an inductive set. This description should use an existential quantifier.

2. Use the definition of an inductive set to determine which of the following sets are inductive sets and which are not. Do not worry about formal proofs, but if a set is not inductive, be sure to provide a specific counterexample that proves it is not inductive.

   1. $A=\{1,2,3,\mathrm{\dots },20\}$

   2. The set of natural numbers, $\mathbb{N}$

   3. $B=\{n\in \mathbb{N}\mid n\ge 5\}$

   4. $S=\{n\in \mathbb{Z}\mid n\ge -3\}$

   5. $R=\{n\in \mathbb{Z}\mid n\le 100\}$

   6. The set of integers, $\mathbb{Z}$

   7. The set of odd natural numbers.

3. This part will explore one of the underlying mathematical ideas for a proof by induction. Assume that $T\subseteq \mathbb{N}$ and assume that $1\in T$ and that $T$ is an inductive set. Use the definition of an inductive set to answer each of the following:

   1. Is $2\in T$? Explain.

   2. Is $100\in T$? Explain.

   3. Is $3\in T$? Explain.

   4. Is $4\in T$? Explain.

   5. Do you think that $T=\mathbb{N}$? Explain.

4.1.2 Inductive Sets

The two open sentences in Beginning Activity 1 appeared to be true for all values of $n$ in the set of natural numbers, $\mathbb{N}$. That is, the examples in this beginning activity provided evidence that the following two statements are true.

• For each natural number $n,4$ divides $\left(5^n-1\right)$.

• For each natural number $n,1^2+2^2+\mathrm{\cdots }+n^2=\frac{n(n+1)(2n+1)}{6}$.

One way of proving statements of this form uses the concept of an inductive set introduced in Beginning Activity 2. The idea is to prove that if one natural number
makes the open sentence true, then the next one also makes the open sentence true. This is how we handle the phrase "and so on" when dealing with the natural numbers. In Beginning Activity 2, we saw that the number systems $\mathbb{N}$ and $\mathbb{Z}$ and other sets are inductive. What we are trying to do is somehow distinguish $\mathbb{N}$ from the other inductive sets. The way to do this was suggested in Part (3) of Beginning Activity 2. Although we will not prove it, the following statement should seem true.

Statement 1: For each subset $T$ of $\mathbb{N}$, if $1\in T$ and $T$ is inductive, then $T=\mathbb{N}$.

Notice that the integers, $\mathbb{Z}$, and the set $S=\{n\in \mathbb{Z}\mid n\ge -3\}$ both contain 1 and both are inductive, but they both contain numbers other than natural numbers. For example, the following statement is false:

Statement 2: For each subset $T$ of $\mathbb{Z}$, if $1\in T$ and $T$ is inductive, then $T=\mathbb{Z}$.

The set $S=\{n\in \mathbb{Z}\mid n\ge -3\}=\{-3,-2,-1,0,1,2,3,\mathrm{\dots }\}$ is a counterexample that shows that this statement is false.

4.1.3 Progress Check 4.1 (Inductive Sets)

Suppose that $T$ is an inductive subset of the integers. Which of the following statements are true, which are false, and for which ones is it not possible to tell?

1. $1\in T$ and $5\in T$.

2. If $1\in T$, then $5\in T$.

3. If $5\notin T$, then $2\notin T$.

4. For each integer $k$, if $k\in T$, then $k+7\in T$.

5. For each integer $k,k\notin T$ or

$$k+1\in T.$$

1. There exists an integer $k$ such that $k\in T$ and $k+1\notin T$.

2. For each integer $k$, if $k+1\in T$, then $k\in T$.

3. For each integer $k$, if $k+1\notin T$, then $k\notin T$.

4.1.4 The Principle of Mathematical Induction

Although we proved that Statement (2) is false, in this text, we will not prove that Statement (1) is true. One reason for this is that we really do not have a formal definition of the natural numbers. However, we should be convinced that

Statement (1) is true. We resolve this by making Statement (1) an axiom for the natural numbers so that this becomes one of the defining characteristics of the natural numbers.

The Principle of Mathematical Induction If $T$ is a subset of $\mathbb{N}$ such that

1. $1\in T$, and

2. For every $k\in \mathbb{N}$, if $k\in T$, then $(k+1)\in T$, then $T=\mathbb{N}$.

4.1.5 Using the Principle of Mathematical Induction

The primary use of the Principle of Mathematical Induction is to prove statements of the form

$$(\forall n\in \mathbb{N})(P(n))$$

where $P(n)$ is some open sentence. Recall that a universally quantified statement like the preceding one is true if and only if the truth set $T$ of the open sentence $P(n)$ is the set $\mathbb{N}$. So our goal is to prove that $T=\mathbb{N}$, which is the conclusion of the Principle of Mathematical Induction. To verify the hypothesis of the Principle of Mathematical Induction, we must

1. Prove that $1\in T$. That is, prove that $P(1)$ is true.

2. Prove that if $k\in T$, then $(k+1)\in T$. That is, prove that if $P(k)$ is true, then $P(k+1)$ is true.

The first step is called the basis step or the initial step, and the second step is called the inductive step. This means that a proof by mathematical induction will have the following form:

4.1.6 Procedure for a Proof by Mathematical Induction

To prove: $(\forall n\in \mathbb{N})(P(n))$

Basis step: Prove $P(1)$.
Inductive step: Prove that for each $k\in \mathbb{N}$, if $P(k)$ is true, then $P(k+1)$ is true.

We can then conclude that $P(n)$ is true for all $n\in \mathbb{N}$.

Note that in the inductive step, we want to prove that the conditional statement "for each $k\in \mathbb{N}$, if $P(k)$ then $P(k+1)$" is true. So we will start the inductive step by assuming that $P(k)$ is true. This assumption is called the inductive assumption or the inductive hypothesis.

The key to constructing a proof by induction is to discover how $P(k+1)$ is related to $P(k)$ for an arbitrary natural number $k$. For example, in Beginning Activity 1, one of the open sentences $P(n)$ was

$$1^2+2^2+\mathrm{\cdots }+n^2=\frac{n(n+1)(2n+1)}{6}.$$

Sometimes it helps to look at some specific examples such as $P(2)$ and $P(3)$. The idea is not just to do the computations, but to see how the statements are related. This can sometimes be done by writing the details instead of immediately doing computations.

$P(2)$ is $1^2+2^2$ $={\displaystyle \frac{2\cdot 3\cdot 5}{6}}$

$P(3)$ is $1^2+2^2+3^2$ $={\displaystyle \frac{3\cdot 4\cdot 7}{6}}$

In this case, the key is the left side of each equation. The left side of $P(3)$ is obtained from the left side of $P(2)$ by adding one term, which is $3^2$. This suggests that we might be able to obtain the equation for $P(3)$ by adding $3^2$ to both sides of the equation in $P(2)$. Now for the general case, if $k\in \mathbb{N}$, we look at $P(k+1)$ and compare it to $P(k)$.

$P(k)$ is $1^2+2^2+\mathrm{\cdots }+k^2$ $={\displaystyle \frac{k(k+1)(2k+1)}{6}}$

$P(k+1)$ is $1^2+2^2+\mathrm{\cdots }+{(k+1)}^2$ $={\displaystyle \frac{(k+1)[(k+1)+1][2(k+1)+1]}{6}}$

The key is to look at the left side of the equation for $P(k+1)$ and realize what this notation means. It means that we are adding the squares of the first $(k+1)$ natural numbers. This means that we can write

$$1^2+2^2+\mathrm{\cdots }+{(k+1)}^2=1^2+2^2+\mathrm{\cdots }+k^2+{(k+1)}^2.$$

This shows us that the left side of the equation for $P(k+1)$ can be obtained from the left side of the equation for $P(k)$ by adding ${(k+1)}^2$. This is the motivation for proving the inductive step in the following proof.

Proposition 4.2. For each natural number $n$,

$$1^2+2^2+\mathrm{\cdots }+n^2=\frac{n(n+1)(2n+1)}{6}.$$

Proof. We will use a proof by mathematical induction. For each natural number $n$, we let $P(n)$ be

$$1^2+2^2+\mathrm{\cdots }+n^2=\frac{n(n+1)(2n+1)}{6}$$

We first prove that $P(1)$ is true. Notice that $\frac{1(1+1)(2\cdot 1+1)}{6}=1$. This shows that

$$1^2=\frac{1(1+1)(2\cdot 1+1)}{6},$$

which proves that $P(1)$ is true.
For the inductive step, we prove that for each $k\in \mathbb{N}$, if $P(k)$ is true, then $P(k+1)$ is true. So let $k$ be a natural number and assume that $P(k)$ is true. That is, assume that

$$1^2+2^2+\mathrm{\cdots }+k^2=\frac{k(k+1)(2k+1)}{6}.$$ (1)

The goal now is to prove that $P(k+1)$ is true. That is, it must be proved that

$1^2+2^2+\mathrm{\cdots }+k^2+{(k+1)}^2$ $={\displaystyle \frac{(k+1)[(k+1)+1][2(k+1)+1]}{6}}$

$={\displaystyle \frac{(k+1)(k+2)(2k+3)}{6}}$ (2)

To do this, we add ${(k+1)}^2$ to both sides of equation (1) and algebraically rewrite the right side of the resulting equation. This gives

$1^2+2^2+\mathrm{\cdots }+k^2+{(k+1)}^2$ $={\displaystyle \frac{k(k+1)(2k+1)}{6}}+{(k+1)}^2$

$={\displaystyle \frac{k(k+1)(2k+1)+6{(k+1)}^2}{6}}$

$={\displaystyle \frac{(k+1)[k(2k+1)+6(k+1)]}{6}}$

$={\displaystyle \frac{(k+1)\left(2k^2+7k+6\right)}{6}}$

$={\displaystyle \frac{(k+1)(k+2)(2k+3)}{6}}$

Comparing this result to equation (2), we see that if $P(k)$ is true, then $P(k+1)$ is true. Hence, the inductive step has been established, and by the Principle of Mathematical Induction, we have proved that for each natural number $n$, $1^2+2^2+\mathrm{\cdots }+n^2=\frac{n(n+1)(2n+1)}{6}$.

4.1.7 Writing Guideline

The proof of Proposition 4.2 shows a standard way to write an induction proof. When writing a proof by mathematical induction, we should follow the guideline that we always keep the reader informed. This means that at the beginning of the proof, we should state that a proof by induction will be used. We should then clearly define the open sentence $P(n)$ that will be used in the proof.

4.1.8 Summation Notation

The result in Proposition 4.2 could be written using summation notation as follows:

$$\text{ For each natural number }n,\sum _{j=1}^n{j}^2=\frac{n(n+1)(2n+1)}{6}.$$

In this case, we use $j$ for the index for the summation, and the notation ${\sum }_{j=1}^n{j}^2$ tells us to add all the values of $j^2$ for $j$ from 1 to $n$, inclusive. That is,

$$\sum _{j=1}^n{j}^2=1^2+2^2+\mathrm{\cdots }+n^2$$

So in the proof of Proposition 4.2, we would let $P(n)$ be ${\sum }_{j=1}^n{j}^2=\frac{n(n+1)(2n+1)}{6}$, and we would use the fact that for each natural number $k$,

$$\sum _{j=1}^{k+1}{j}^2=\left(\sum _{j=1}^k{j}^2\right)+{(k+1)}^2$$

4.1.9 Progress Check 4.3 (An Example of a Proof by Induction)

1. Calculate $1+2+3+\mathrm{\cdots }+n$ and $\frac{n(n+1)}{2}$ for several natural numbers $n$. What do you observe?

2. Use mathematical induction to prove that $1+2+3+\mathrm{\cdots }+n=\frac{n(n+1)}{2}$.

To do this, let $P(n)$ be the open sentence," $1+2+3+\mathrm{\cdots }+n=\frac{n(n+1)}{2}$." For the basis step, notice that the equation $1=\frac{1(1+1)}{2}$ shows that $P(1)$ is true. Now let $k$ be a natural number and assume that $P(k)$ is true. That is, assume that

$$1+2+3+\mathrm{\cdots }+k=\frac{k(k+1)}{2}$$

and complete the proof.

4.1.10 Some Comments about Mathematical Induction

1. The basis step is an essential part of a proof by induction. See Exercise (19) for an example that shows that the basis step is needed in a proof by induction.

2. Exercise (20) provides an example that shows the inductive step is also an essential part of a proof by mathematical induction.

3. It is important to remember that the inductive step in an induction proof is a proof of a conditional statement. Although we did not explicitly use the forward-backward process in the inductive step for Proposition 4.2, it was implicitly used in the discussion prior to Proposition 4.2. The key question was, "How does knowing the sum of the first $k$ squares help us find the sum of the first $(k+1)$ squares?"

4. When proving the inductive step in a proof by induction, the key question is,

$$\text{ How does knowing }P(k)\text{ help us prove }P(k+1)\text{? }$$

In Proposition 4.2, we were able to see that the way to answer this question was to add a certain expression to both sides of the equation given in $P(k)$. Sometimes the relationship between $P(k)$ and $P(k+1)$ is not as easy to see. For example, in Beginning Activity 1, we explored the following proposition:

For each natural number $n,4$ divides $\left(5^n-1\right)$.

This means that the open sentence, $P(n)$, is "4 divides ($5^n-1$)." So in the inductive step, we assume $k\in \mathbb{N}$ and that 4 divides $\left(5^k-1\right)$. This means that there exists an integer $m$ such that

$$5^k-1=4m.$$ (1)

In the backward process, the goal is to prove that 4 divides $\left(5^{k+1}-1\right)$. This can be accomplished if we can prove that there exists an integer $s$ such that

$$5^{k+1}-1=4s.$$ (2)

We now need to see if there is anything in equation (1) that can be used in equation (2). The key is to find something in the equation $5^k-1=4m$ that is related to something similar in the equation $5^{k+1}-1=4s$. In this case, we notice that

$$5^{k+1}=5\cdot 5^k$$

So if we can solve $5^k-1=4m$ for $5^k$, we could make a substitution for $5^k$. This is done in the proof of the following proposition.

Proposition 4.4. For every natural number $n$, 4 divides $\left(5^n-1\right)$.

Proof. (Proof by Mathematical Induction) For each natural number $n$, let $P(n)$ be "4 divides $\left(5^n-1\right)$." We first prove that $P(1)$ is true. Notice that when $n=1$, $\left(5^n-1\right)=4$. Since 4 divides 4, $P(1)$ is true.

For the inductive step, we prove that for all $k\in \mathbb{N}$, if $P(k)$ is true, then $P(k+1)$ is true. So let $k$ be a natural number and assume that $P(k)$ is true. That is, assume that

$$4\text{ divides }\left(5^k-1\right)$$

This means that there exists an integer $m$ such that

$$5^k-1=4m.$$

Thus,

$$5^k=4m+1.$$ (1)

In order to prove that $P(k+1)$ is true, we must show that 4 divides $\left(5^{k+1}-1\right)$. Since $5^{k+1}=5\cdot 5^k$, we can write

$$5^{k+1}-1=5\cdot 5^k-1$$ (2)

We now substitute the expression for $5^k$ from equation (1) into equation (2). This gives

$5^{k+1}-1$ $=5\cdot 5^k-1$

$=5(4m+1)-1$

$=(20m+5)-1$

$=20m+4$

$=4(5m+1)$ (3)

Since $(5m+1)$ is an integer, equation (3) shows that 4 divides $\left(5^{k+1}-1\right)$. Therefore, if $P(k)$ is true, then $P(k+1)$ is true and the inductive step has been established. Thus, by the Principle of Mathematical Induction, for every natural number $n,4$ divides $\left(5^n-1\right)$.

Proposition 4.4 was stated in terms of "divides." We can use congruence to state a proposition that is equivalent to Proposition 4.4. The idea is that the sentence, 4 divides $\left(5^n-1\right)$ means that $5^n\equiv 1(mod4)$. So the following proposition is equivalent to Proposition 4.4.

Proposition 4.5. For every natural number $n,5^n\equiv 1(mod4)$.

Since we have proved Proposition 4.4, we have in effect proved Proposition 4.5. However, we could have proved Proposition 4.5 first by using the results in Theorem 3.28. This will be done in the next progress check.

4.1.11 Progress Check 4.6 (Proof of Proposition 4.5)

To prove Proposition 4.5, we let $P(n)$ be $5^n\equiv 1(mod4)$ and notice that $P(1)$ is true since $5\equiv 1(mod4)$. For the inductive step, let $k$ be a natural number and assume that $P(k)$ is true. That is, assume that $5^k\equiv 1(mod4)$.

1. What must be proved in order to prove that $P(k+1)$ is true?

2. Since $5^{k+1}=5\cdot 5^k$, multiply both sides of the congruence $5^k\equiv 1(mod4)$ by 5. The results in Theorem 3.28 justify this step.

3. Now complete the proof that for each $k\in \mathbb{N}$, if $P(k)$ is true, then $P(k+1)$ is true and complete the induction proof of Proposition 4.5.

It might be nice to compare the proofs of Propositions 4.4 and 4.5 and decide which one is easier to understand.

4.1.12 Exercises for Section 4.1

1. $(\star )$ Which of the following sets are inductive sets? Explain.

   1. $\mathbb{Z}$

   2. $\{x\in \mathbb{N}\mid x\ge 4\}$

   3. $\{x\in \mathbb{Z}\mid x\le 10\}$

   4. $\{1,2,3,\mathrm{\dots },500\}$

2. $(\star )$

   1. Can a finite, nonempty set be inductive? Explain.

   2. Is the empty set inductive? Explain.

3. Use mathematical induction to prove each of the following:

   1. $(\star )$ For each natural number $n,2+5+8+\mathrm{\cdots }+(3n-1)=\frac{n(3n+1)}{2}$.

   2. For each natural number $n,1+5+9+\mathrm{\cdots }+(4n-3)=n(2n-1)$.

   3. For each natural number $n,1^3+2^3+3^3+\mathrm{\cdots }+n^3={\left[\frac{n(n+1)}{2}\right]}^2$.

4. Based on the results in Progress Check 4.3 and Exercise (3c), if $n\in \mathbb{N}$, is there any conclusion that can be made about the relationship between the sum $\left(1^3+2^3+3^3+\mathrm{\cdots }+n^3\right)$ and the sum $(1+2+3+\mathrm{\cdots }+n)$?

5. Instead of using induction, we can sometimes use previously proven results about a summation to obtain results about a different summation.

   1. Use the result in Progress Check 4.3 to prove the following proposition:

      $$\text{ For each natural number }n,3+6+9+\mathrm{\cdots }+3n=\frac{3n(n+1)}{2}.$$

   2. Subtract $n$ from each side of the equation in Part (a). On the left side of this equation, explain why this can be done by subtracting 1 from each term in the summation.

   3. Algebraically simplify the right side of the equation in Part (b) to obtain a formula for the sum $2+5+8+\mathrm{\cdots }+(3n-1)$. Compare this to Exercise (3a).

6. $(\star )$

   1. Calculate $1+3+5+\mathrm{\cdots }+(2n-1)$ for several natural numbers $n$.

   2. Based on your work in Exercise (6a), if $n\in \mathbb{N}$, make a conjecture about the value of the sum $1+3+5+\mathrm{\cdots }+(2n-1)={\sum }_{j=1}^n(2j-1)$.

   3. Use mathematical induction to prove your conjecture in Exercise (6b).

7. In Section 3.1, we defined congruence modulo $n$ for a natural number $n$, and in Section 3.5, we used the Division Algorithm to prove that each integer is congruent, modulo $n$, to precisely one of the integers $0,1,2,\mathrm{\dots },n-1$ (Corollary 3.32).

   1. Find the value of $r$ so that $4\equiv r(mod3)$ and $r\in \{0,1,2\}$.

   2. Find the value of $r$ so that $4^2\equiv r(mod3)$ and $r\in \{0,1,2\}$.

   3. Find the value of $r$ so that $4^3\equiv r(mod3)$ and $r\in \{0,1,2\}$.

   4. For two other values of $n$, find the value of $r$ so that $4^n\equiv r(mod3)$ and $r\in \{0,1,2\}$.

   5. $(\star )$ If $n\in \mathbb{N}$, make a conjecture concerning the value of $r$ where $4^n\equiv r(mod3)$ and $r\in \{0,1,2\}$. This conjecture should be written as a self-contained proposition including an appropriate quantifier.

   6. $(\star )$ Use mathematical induction to prove your conjecture.

8. Use mathematical induction to prove each of the following:

   1. $(\star )$ For each natural number $n,3$ divides ($4^n-1$).

   2. For each natural number $n,6$ divides $\left(n^3-n\right)$.

9. In Exercise (7), we proved that for each natural number $n,4^n\equiv 1(mod3)$. Explain how this result is related to the proposition in Exercise (8a).

10. Use mathematical induction to prove that for each natural number $n,3$ divides $n^3+23n$. Compare this proof to the proof from Exercise (19) in Section 3.5.

11. 1. Calculate the value of $5^n-2^n$ for $n=1,n=2,n=3,n=4,n=5$, and $n=6$.

    2. Based on your work in Part (a), make a conjecture about the values of $5^n-2^n$ for each natural number $n$.

    3. Use mathematical induction to prove your conjecture in Part (b).

12. Let $x$ and $y$ be distinct integers. Prove that for each natural number $n$, $(x-y)$ divides $\left(x^n-y^n\right)$. Explain why your conjecture in Exercise (11) is a special case of this result.

13. $(\star )$ Prove Part (3) of Theorem 3.28 from Section 3.4. Let $n\in \mathbb{N}$ and let $a$ and $b$ be integers. For each $m\in \mathbb{N}$, if $a\equiv b(modn)$, then $a^m\equiv b^m(modn)$.

14. $(\star )$ Use mathematical induction to prove that the sum of the cubes of any three consecutive natural numbers is a multiple of 9.

15. Let $a$ be a real number. We will explore the derivatives of the function $f(x)=e^{ax}$. By using the chain rule, we see

    $$\frac{d}{dx}\left(e^{ax}\right)=a{e}^{ax}$$

    Recall that the second derivative of a function is the derivative of the derivative function. Similarly, the third derivative is the derivative of the second derivative.

    1. What is $\frac{d^2}{d{x}^2}\left(e^{ax}\right)$, the second derivative of $e^{ax}$?

    2. What is $\frac{d^3}{d{x}^3}\left(e^{ax}\right)$, the third derivative of $e^{ax}$?

    3. Let $n$ be a natural number. Make a conjecture about the $n^{\text{th }}$ derivative of the function $f(x)=e^{ax}$. That is, what is $\frac{d^n}{d{x}^n}\left(e^{ax}\right)$? This conjecture should be written as a self-contained proposition including an appropriate quantifier.

    4. Use mathematical induction to prove your conjecture.

16. In calculus, it can be shown that

    ${\displaystyle \int {\sin }^{2}xdx}={\displaystyle \frac{x}{2}}-{\displaystyle \frac{1}{2}}\sin x\cos x+c\text{ and}$

    ${\displaystyle \int {\cos }^{2}xdx}={\displaystyle \frac{x}{2}}+{\displaystyle \frac{1}{2}}\sin x\cos x+c$

    Using integration by parts, it is also possible to prove that for each natural number $n$,

    ${\displaystyle \int {\sin }^{n}xdx}=-{\displaystyle \frac{1}{n}}{\sin }^{n-1}x\cos x+{\displaystyle \frac{n-1}{n}}{\displaystyle \int {\sin }^{n-2}xdx}\text{ and}$

    ${\displaystyle \int {\cos }^{n}xdx}={\displaystyle \frac{1}{n}}{\cos }^{n-1}x\sin x+{\displaystyle \frac{n-1}{n}}{\displaystyle \int {\cos }^{n-2}xdx}$

    1. Determine the values of

       $${\int }_0^{\pi /2}{\sin }^{2}xdx\text{ and }{\int }_0^{\pi /2}{\sin }^{4}xdx$$

    2. Use mathematical induction to prove that for each natural number $n$,

       ${\displaystyle {\int }_0^{\pi /2}}{\sin }^{2n}xdx$ $={\displaystyle \frac{1\cdot 3\cdot 5\mathrm{\cdots }(2n-1)}{2\cdot 4\cdot 6\mathrm{\cdots }(2n)}}{\displaystyle \frac{\pi }{2}}\text{ and}$

       ${\displaystyle {\int }_0^{\pi /2}}{\sin }^{2n+1}xdx$ $={\displaystyle \frac{2\cdot 4\cdot 6\mathrm{\cdots }(2n)}{1\cdot 3\cdot 5\mathrm{\cdots }(2n+1)}}$

       These are known as the Wallis sine formulas.

    3. Use mathematical induction to prove that

       ${\displaystyle {\int }_0^{\pi /2}}{\cos }^{2n}xdx$ $={\displaystyle \frac{1\cdot 3\cdot 5\mathrm{\cdots }(2n-1)}{2\cdot 4\cdot 6\mathrm{\cdots }(2n)}}{\displaystyle \frac{\pi }{2}}\text{ and}$

       ${\displaystyle {\int }_0^{\pi /2}}{\cos }^{2n+1}xdx$ $={\displaystyle \frac{2\cdot 4\cdot 6\mathrm{\cdots }(2n)}{1\cdot 3\cdot 5\mathrm{\cdots }(2n+1)}}$

       These are known as the Wallis cosine formulas.

17. 1. Why is it not possible to use mathematical induction to prove a proposition of the form

       $$(\forall x\in \mathbb{Q})(P(x)),$$

       where $P(x)$ is some predicate?

    2. Why is it not possible to use mathematical induction to prove a proposition of the form

       For each real number $x$ with $x\ge 1,P(x)$, where $P(x)$ is some predicate?

18. Evaluation of proofs. See the instructions for Exercise (19) from Section 3.1.

    1. For each natural number $n,1+4+7+\mathrm{\cdots }+(3n-2)=\frac{n(3n-1)}{2}$.

       Proof. We will prove this proposition using mathematical induction. So we let $P(n)$ be the open sentence

       $$1+4+7+\mathrm{\cdots }+(3n-2)$$

       Using $n=1$, we see that $3n-2=1$ and hence, $P(1)$ is true.
       We now assume that $P(k)$ is true. That is,

       $$1+4+7+\mathrm{\cdots }+(3k-2)=\frac{k(3k-1)}{2}$$

       We then see that

       $1+4+7+\mathrm{\cdots }+(3k-2)+(3(k+1)-2)$ $={\displaystyle \frac{(k+1)(3k+2)}{2}}$

       ${\displaystyle \frac{k(3k-1)}{2}}+(3k+1)$ $={\displaystyle \frac{(k+1)(3k+2)}{2}}$

       ${\displaystyle \frac{\left(3k^2-k\right)+(6k+2)}{2}}$ $={\displaystyle \frac{3k^2+5k+2}{2}}$

       ${\displaystyle \frac{3k^2+5k+2}{2}}$ $={\displaystyle \frac{3k^2+5k+2}{2}}$

       We have thus proved that $P(k+1)$ is true, and hence, we have proved the proposition.

    2. For each natural number $n,1+4+7+\mathrm{\cdots }+(3n-2)=\frac{n(3n-1)}{2}$.

       Proof. We will prove this proposition using mathematical induction. So we let

       $$P(n)=1+4+7+\mathrm{\cdots }+(3n-2).$$

       Using $n=1$, we see that $P(1)=1$ and hence, $P(1)$ is true.
       We now assume that $P(k)$ is true. That is,

       $$1+4+7+\mathrm{\cdots }+(3k-2)=\frac{k(3k-1)}{2}.$$

       We then see that

       $P(k+1)$ $=1+4+7+\mathrm{\cdots }+(3k-2)+(3(k+1)-2)$

       $={\displaystyle \frac{k(3k-1)}{2}}+3(k+1)-2$

       $={\displaystyle \frac{3k^2-k+6k+6-4}{2}}$

       $={\displaystyle \frac{3k^2+5k+2}{2}}$

       $={\displaystyle \frac{(k+1)(3k+2)}{2}}.$

       We have thus proved that $P(k+1)$ is true, and hence, we have proved the proposition.

    3. All dogs are the same breed.

       Proof. We will prove this proposition using mathematical induction. For each natural number $n$, we let $P(n)$ be

       Any set of $n$ dogs consists entirely of dogs of the same breed.
       We will prove that for each natural number $n,P(n)$ is true, which will prove that all dogs are the same breed. A set with only one dog consists entirely of dogs of the same breed and, hence, $P(1)$ is true.
       So we let $k$ be a natural number and assume that $P(k)$ is true, that is, that every set of $k$ dogs consists of dogs of the same breed. Now consider a set $D$ of $k+1$ dogs, where

       $$D=\{d_1,d_2,\mathrm{\dots },d_k,d_{k+1}\}$$

       If we remove the $\mathrm{dog}{d}_1$ from the set $D$, we then have a set $D_1$ of $k$ dogs, and using the assumption that $P(k)$ is true, these dogs must all be of the same breed. Similarly, if we remove $d_{k+1}$ from the set $D$, we again have a set $D_2$ of $k$ dogs, and these dogs must all be of the same breed. Since $D=D_1\cup D_2$, we have proved that all of the dogs in $D$ must be of the same breed.
       This proves that if $P(k)$ is true, then $P(k+1)$ is true and, hence, by mathematical induction, we have proved that for each natural number $n$, any set of $n$ dogs consists entirely of dogs of the same breed.

4.1.13 Explorations and Activities

1. The Importance of the Basis Step. Most of the work done in constructing a proof by induction is usually in proving the inductive step. This was certainly the case in Proposition 4.2. However, the basis step is an essential part of the proof. Without it, the proof is incomplete. To see this, let $P(n)$ be

   $$1+2+\mathrm{\cdots }+n=\frac{n^2+n+1}{2}$$

   1. Let $k\in \mathbb{N}$. Complete the following proof that if $P(k)$ is true, then $P(k+1)$ is true.
      Let $k\in \mathbb{N}$. Assume that $P(k)$ is true. That is, assume that

      $$1+2+\mathrm{\cdots }+k=\frac{k^2+k+1}{2}$$ (1)

      The goal is to prove that $P(k+1)$ is true. That is, we need to prove that

      $$1+2+\mathrm{\cdots }+k+(k+1)=\frac{{(k+1)}^2+(k+1)+1}{2}$$ (2)

      To do this, we add $(k+1)$ to both sides of equation (1). This gives

      $1+2+\mathrm{\cdots }+k+(k+1)$ $={\displaystyle \frac{k^2+k+1}{2}}+(k+1)$

      $=\mathrm{\cdots }$

   2. Is $P(1)$ true? Is $P(2)$ true? What about $P(3)$ and $P(4)$? Explain how this shows that the basis step is an essential part of a proof by induction.

2. Regions of a Circle. Place $n$ equally spaced points on a circle and connect each pair of points with the chord of the circle determined by that pair of points. See Figure 4.1.

   

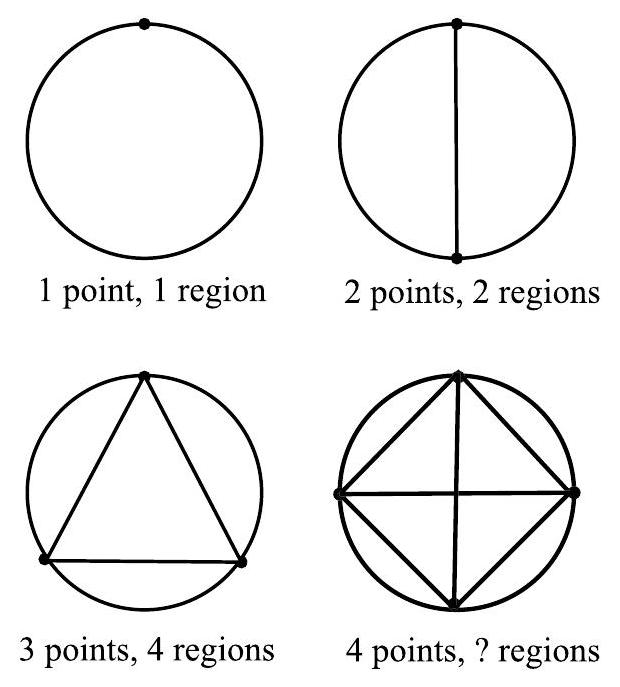
   Figure 4.1: Regions of Circles

   Count the number of distinct regions within each circle. For example, with three points on the circle, there are four distinct regions. Organize your data in a table with two columns: "Number of Points on the Circle" and "Number of Distinct Regions in the Circle."

   1. How many regions are there when there are four equally spaced points on the circle?

   2. Based on the work so far, make a conjecture about how many distinct regions would you get with five equally spaced points.

   3. Based on the work so far, make a conjecture about how many distinct regions would you get with six equally spaced points.

   4. Figure 4.2 shows the figures associated with Parts (b) and (c). Count the number of regions in each case. Are your conjectures correct or incorrect?

   5. Explain why this activity shows that the inductive step is an essential part of a proof by mathematical induction.

      

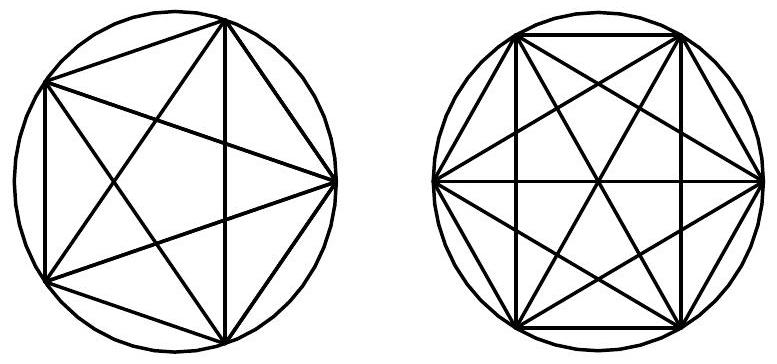
      Figure 4.2: Regions of Circles