5 Set Theory

5.5 Indexed Families of Sets

5.5.1 Beginning Activity 1 (The Union and Intersection of a Family of Sets)

In Section 5.3, we discussed various properties of set operations. We will now focus on the associative properties for set union and set intersection. Notice that the definition of "set union" tells us how to form the union of two sets. It is the associative law that allows us to discuss the union of three sets. Using the associate law, if $A,B$, and $C$ are subsets of some universal set, then we can define $A\cup B\cup C$ to be $(A\cup B)\cup C$ or $A\cup (B\cup C)$. That is,

$$A\cup B\cup C=(A\cup B)\cup C=A\cup (B\cup C).$$

For this activity, the universal set is $\mathbb{N}$ and we will use the following four sets:
$A=\{1,2,3,4,5\}$
$C=\{3,4,5,6,7\}$
$B=\{2,3,4,5,6\}$
$D=\{4,5,6,7,8\}$.

1. Use the roster method to specify the sets $A\cup B\cup C,B\cup C\cup D,A\cap B\cap C$, and $B\cap C\cap D$.

2. Use the roster method to specify each of the following sets. In each case, be sure to follow the order specified by the parentheses.

   1. $(A\cup B\cup C)\cup D$

   2. $A\cup (B\cup C\cup D)$

   3. $A\cup (B\cup C)\cup D$

   4. $(A\cup B)\cup (C\cup D)$

   5. $(A\cap B\cap C)\cap D$

   6. $A\cap (B\cap C\cap D)$

   7. $A\cap (B\cap C)\cap D$

   8. $(A\cap B)\cap (C\cap D)$

3. Based on the work in Part (2), does the placement of the parentheses matter when determining the union (or intersection) of these four sets? Does this make it possible to define $A\cup B\cup C\cup D$ and $A\cap B\cap C\cap D$ ?

We have already seen that the elements of a set may themselves be sets. For example, the power set of a set $T,𝒫(T)$, is the set of all subsets of $T$. The phrase, "a set of sets" sounds confusing, and so we often use the terms collection and family when we wish to emphasize that the elements of a given set are themselves sets. We would then say that the power set of $T$ is the family (or collection) of sets that are subsets of $T$.

One of the purposes of the work we have done so far in this activity was to show that it is possible to define the union and intersection of a family of sets.

Definition. Let $𝒞$ be a family of sets. The union of $𝒞$ is defined as the set of all elements that are in at least one of the sets in $𝒞$. We write

$$\bigcup _{X\in ℭ}X=\{x\in U\mid x\in X\text{ for some }X\in 𝒞\}$$

The intersection of $𝒞$ is defined as the set of all elements that are in all of the sets in $𝒞$. That is,

$$\bigcap _{X\in 𝒞}X=\{x\in U\mid x\in X\text{ for all }X\in 𝒞\}$$

For example, consider the four sets $A,B,C$, and $D$ used earlier in this activity and the sets

$$S=\{5,6,7,8,9\}\text{ and }T=\{6,7,8,9,10\}.$$

We can then consider the following families of sets: $𝒜=\{A,B,C,D\}$ and $ℬ=\{A,B,C,D,S,T\}$.

1. Explain why

   $$\bigcup _{X\in 𝒜}X=A\cup B\cup C\cup D\text{ and }\bigcap _{X\in 𝒜}X=A\cap B\cap C\cap D,$$

   and use your work in (1), (2), and (3) to determine ${\bigcup }_{X\in 𝒜}X$ and ${\bigcap }_{X\in 𝒜}X$.

2. Use the roster method to specify ${\bigcup }_{X\in ℬ}X$ and ${\bigcap }_{X\in ℬ}X$.

3. Use the roster method to specify the sets ${\left({\bigcup }_{X\in 𝒜}X\right)}^c$ and ${\bigcap }_{X\in 𝒜}{X}^c$. Remember that the universal set is $\mathbb{N}$.

5.5.2 Beginning Activity 2 (An Indexed Family of Sets)

We often use subscripts to identify sets. For example, in Beginning Activity 1, instead of using $A,B,C$, and $D$ as the names of the sets, we could have used $A_1$, $A_2,A_3$, and $A_4$. When we do this, we are using the subscript as an identifying tag, or index, for each set. We can also use this idea to specify an infinite family of sets. For example, for each natural number $n$, we define

$$C_n=\{n,n+1,n+2,n+3,n+4\}.$$

So if we have a family of sets $𝒞=\{C_1,C_2,C_3,C_4\}$, we use the notation ${\bigcup }_{j=1}^4{C}_j$ to mean the same thing as ${\bigcup }_{X\in ℭ}X$.

1. Determine ${\bigcup }_{j=1}^4{C}_j$ and ${\bigcap }_{j=1}^4{C}_j$.

We can see that with the use of subscripts, we do not even have to define the family of sets $𝒜$. We can work with the infinite family of sets

$${𝒞}^{\ast }=\{A_n\mid n\in \mathbb{N}\}$$

and use the subscripts to indicate which sets to use in a union or an intersection.

1. Use the roster method to specify each of the following pairs of sets. The universal set is $\mathbb{N}$.

   1. ${\bigcup }_{j=1}^6{C}_j$ and ${\bigcap }_{j=1}^6{C}_j$

   2. ${\bigcup }_{j=1}^8{C}_j$ and ${\bigcap }_{j=1}^8{C}_j$

   3. ${\bigcup }_{j=4}^8{C}_j$ and ${\bigcap }_{j=4}^8{C}_j$

   4. ${\left({\bigcap }_{j=1}^4{C}_j\right)}^c$ and ${\bigcup }_{j=1}^4{C}_j^c$

5.5.3 The Union and Intersection of an Indexed Family of Sets

One of the purposes of the beginning activities was to show that we often encounter situations in which more than two sets are involved, and it is possible to define the union and intersection of more than two sets. In Beginning Activity 2, we also saw that it is often convenient to "index" the sets in a family of sets. In particular, if $n$ is a natural number and $𝒜=\{A_1,A_2,\mathrm{\dots },A_n\}$ is a family of $n$ sets, then the union of these $n$ sets, denoted by $A_1\cup A_2\cup \mathrm{\cdots }\cup A_n$ or ${\bigcup }_{j=1}^n{A}_j$, is defined as

$$\bigcup _{j=1}^n{A}_j=\{x\in U\mid x\in A_j,\text{ for some }j\text{ with }1\le j\le n\}.$$

We can also define the intersection of these $n$ sets, denoted by $A_1\cap A_2\cap \mathrm{\cdots }\cap A_n$ or ${\bigcap }_{j=1}^n{A}_j$, as

$$\bigcap _{j=1}^n{A}_j=\{x\in U\mid x\in A_j,\text{ for all }j\text{ with }1\le j\le n\}.$$

We can also extend this idea to define the union and intersection of a family that consists of infinitely many sets. So if $ℬ=\{B_1,B_2,\mathrm{\dots },B_n,\mathrm{\dots }\}$, then

${\displaystyle \bigcup _{j=1}^{\mathrm{\infty }}}{B}_j=\{x\in U\mid x\in B_j,\text{ for some }j\text{ with }j\ge 1\},\text{ and}$

${\displaystyle \bigcap _{j=1}^{\mathrm{\infty }}}{B}_j=\{x\in U\mid x\in B_j,\text{ for all }j\text{ with }j\ge 1\}$

5.5.4 Progress Check 5.26 (An Infinite Family of Sets)

For each natural number $n$, let $A_n=\{1,n,n^2\}$. For example,

$$A_1=\{1\}{A}_2=\{1,2,4\},A_3=\{1,3,9\}$$

and

$$\bigcup _{j=1}^3{A}_j=\{1,2,3,4,9\},\bigcap _{j=1}^3{A}_j=\{1\}$$

Determine each of the following sets:

1. ${\bigcup }_{j=1}^6{A}_j$

2. ${\bigcap }_{j=1}^6{A}_j$

3. ${\bigcup }_{j=3}^6{A}_j$

4. ${\bigcap }_{j=3}^6{A}_j$

5. ${\bigcup }_{j=1}^{\mathrm{\infty }}{A}_j$

6. ${\bigcap }_{j=1}^{\mathrm{\infty }}{A}_j$

In all of the examples we have studied so far, we have used $\mathbb{N}$ or a subset of $\mathbb{N}$ to index or label the sets in a family of sets. We can use other sets to index or label sets in a family of sets. For example, for each real number $x$, we can define $B_x$ to be the closed interval $[x,x+2]$. That is,

$$B_x=\{y\in ℝ\mid x\le y\le x+2\}$$

So we make the following definition. In this definition, $\mathrm{\Lambda }$ is the uppercase Greek letter lambda and $\alpha$ is the lowercase Greek letter alpha.

Definition. Let $\mathrm{\Lambda }$ be a nonempty set and suppose that for each $\alpha \in \mathrm{\Lambda }$, there is a corresponding set $A_{\alpha }$. The family of sets $\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ is called an indexed family of sets indexed by $\mathrm{\Lambda }$. Each $\alpha \in \mathrm{\Lambda }$ is called an index and $\mathrm{\Lambda }$ is called an indexing set.

5.5.5 Progress Check 5.27 (Indexed Families of Sets)

In each of the indexed families of sets that we seen so far, if the indices were different, then the sets were different. That is, if $\mathrm{\Lambda }$ is an indexing set for the family of sets $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$, then if $\alpha ,\beta \in \mathrm{\Lambda }$ and $\alpha \ne \beta$, then $A_{\alpha }\ne A_{\beta }$. (Note: The letter $\beta$ is the Greek lowercase beta.)

1. Let $\mathrm{\Lambda }=\{1,2,3,4\}$, and for each $n\in \mathrm{\Lambda }$, let $A_n=\{2n+6,16-2n\}$, and let $𝒜=\{A_1,A_2,A_3,A_4\}$. Determine $A_1,A_2,A_3$, and $A_4$.

2. Is the following statement true or false for the indexed family $𝒜$ in (1)?

   For all $m,n\in \mathrm{\Lambda }$, if $m\ne n$, then $A_m\ne A_n$.

3. Now let $\mathrm{\Lambda }=ℝ$. For each $x\in ℝ$, define $B_x=\{0,x^2,x^4\}$. Is the following statement true for the indexed family of sets $ℬ=\{B_x\mid x\in ℝ\}$ ?

   For all $x,y\in ℝ$, if $x\ne y$, then $B_x\ne B_y$.

We now restate the definitions of the union and intersection of a family of sets for an indexed family of sets.

Definition. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets. The union over $𝒜$ is defined as the set of all elements that are in at least one of sets $A_{\alpha }$, where $\alpha \in \mathrm{\Lambda }$. We write

$$\bigcup _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }=\{x\in U\mid \text{ there exists an }\alpha \in \mathrm{\Lambda }\text{ with }x\in A_{\alpha }\}.$$

The intersection over $𝒜$ is the set of all elements that are in all of the sets $A_{\alpha }$ for each $\alpha \in \mathrm{\Lambda }$. That is,

$$\bigcap _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }=\{x\in U\mid \text{ for all }\alpha \in \mathrm{\Lambda },x\in A_{\alpha }\}.$$

5.5.6 Example 5.28 (A Family of Sets Indexed by the Positive Real Numbers)

For each positive real number $\alpha$, let $A_{\alpha }$ be the interval $(-1,\alpha ]$. That is,

If we let ${ℝ}^{+}$be the set of positive real numbers, then we have a family of sets indexed by ${ℝ}^{+}$. We will first determine the union of this family of sets. Notice that for each $\alpha \in {ℝ}^{+},\alpha \in A_{\alpha }$, and if $y$ is a real number with , then $y\in A_{\alpha }$. Also notice that if $y\in ℝ$ and , then for each $\alpha \in {ℝ}^{+},y\notin A_{\alpha }$. With these observations, we conclude that

To determine the intersection of this family, notice that

• if $y\in ℝ$ and , then for each $\alpha \in {ℝ}^{+},y\notin A_{\alpha }$;

• if $y\in ℝ$ and , then $y\in A_{\alpha }$ for each $\alpha \in {ℝ}^{+}$; and

• if $y\in ℝ$ and $y>0$, then if we let $\beta =\frac{y}{2},y>\beta$ and $y\notin A_{\beta }$.

From these observations, we conclude that

5.5.7 Progress Check 5.29 (A Continuation of Example 5.28)

Using the family of sets from Example 5.28, for each $\alpha \in {ℝ}^{+}$, we see that

$$A_{\alpha }^c=(-\mathrm{\infty },-1]\cup (\alpha ,\mathrm{\infty }).$$

Use the results from Example 5.28 to help determine each of the following sets. For each set, use either interval notation or set builder notation.

1. ${\left({\bigcup }_{\alpha \in {ℝ}^{+}}{A}_{\alpha }\right)}^c$

2. ${\bigcap }_{\alpha \in {ℝ}^{+}}{A}_{\alpha }^c$

3. ${\left({\bigcap }_{\alpha \in {ℝ}^{+}}{A}_{\alpha }\right)}^c$

4. ${\bigcup }_{\alpha \in {ℝ}^{+}}{A}_{\alpha }^c$

5.5.8 Properties of Union and Intersection

In Theorem 5.30, we will prove some properties of set operations for indexed families of sets. Some of these properties are direct extensions of corresponding properties for two sets. For example, we have already proved De Morgan’s Laws for two sets in Theorem 5.20. The work in the beginning activities and Progress Check 5.29 suggests that we should get similar results using set operations with an indexed family of sets. For example, in Beginning Activity 2, we saw that

$${\left(\bigcap _{j=1}^4{A}_j\right)}^c=\bigcup _{j=1}^4{A}_j^c.$$

Theorem 5.30. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets, each of which is a subset of some universal set $U$. Then

1. For each $\beta \in \mathrm{\Lambda },{\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\subseteq A_{\beta }$.

2. For each $\beta \in \mathrm{\Lambda },A_{\beta }\subseteq {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$.

3. ${\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$

4. ${\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$

Parts (3) and (4) are known as De Morgan’s Laws.

Proof. We will prove Parts (1) and (3). The proofs of Parts (2) and (4) are included in Exercise (4). So we let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets. To prove Part (1), we let $\beta \in \mathrm{\Lambda }$ and note that if $x\in {\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$, then $x\in A_{\alpha }$, for all $\alpha \in \mathrm{\Lambda }$. Since $\beta$ is one element in $\mathrm{\Lambda }$, we may conclude that $x\in A_{\beta }$. This proves that ${\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\subseteq A_{\beta }$.

To prove Part (3), we will prove that each set is a subset of the other set. We first let $x\in {\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c$. This means that $x\notin \left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)$, and this means that
there exists a $\beta \in \mathrm{\Lambda }$ such that $x\notin A_{\beta }$.
Hence, $x\in A_{\beta }^c$, which implies that $x\in {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$. Therefore, we have proved that

$${\left(\bigcap _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c\subseteq \bigcup _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$$ (1)

We now let $y\in {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$. This means that there exists a $\beta \in \mathrm{\Lambda }$ such that $y\in A_{\beta }^c$ or $y\notin A_{\beta }$. However, since $y\notin A_{\beta }$, we may conclude that $y\notin {\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$ and, hence, $y\in {\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c$. This proves that

$$\bigcup _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c\subseteq {\left(\bigcap _{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c.$$ (2)

Using the results in (1) and (2), we have proved that ${\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$.
Many of the other properties of set operations are also true for indexed families of sets. Theorem 5.31 states the distributive laws for set operations.

Theorem 5.31. Let $\mathrm{\Lambda }$ be a nonempty indexing set, let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets, and let $B$ be a set. Then

1. $B\cap \left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcup }_{\alpha \in \mathrm{\Lambda }}\left(B\cap A_{\alpha }\right)$, and

2. $B\cup \left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcap }_{\alpha \in \mathrm{\Lambda }}\left(B\cup A_{\alpha }\right)$.

The proof of Theorem 5.31 is Exercise (5).

5.5.9 Pairwise Disjoint Families of Sets

In Section 5.2, we defined two sets $A$ and $B$ to be disjoint provided that $A\cap B=\mathrm{\varnothing }$. In a similar manner, if $\mathrm{\Lambda }$ is a nonempty indexing set and $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ is an indexed family of sets, we can say that this indexed family of sets is disjoint
provided that ${\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }=\mathrm{\varnothing }$. However, we can use the concept of two disjoint sets to define a somewhat more interesting type of "disjointness" for an indexed family of sets.

Definition. Let $\mathrm{\Lambda }$ be a nonempty indexing set, and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets. We say that $𝒜$ is pairwise disjoint provided that for all $\alpha$ and $\beta$ in $\mathrm{\Lambda }$, if $A_{\alpha }\ne A_{\beta }$, then $A_{\alpha }\cap A_{\beta }=\mathrm{\varnothing }$.

5.5.10 Progress Check 5.32 (Disjoint Families of Sets)

Figure 5.7 shows two families of sets,

$$𝒜=\{A_1,A_2,A_3,A_4\}\text{ and }ℬ=\{B_1,B_2,B_3,B_4\}.$$

Figure 5.7: Two Families of Indexed Sets

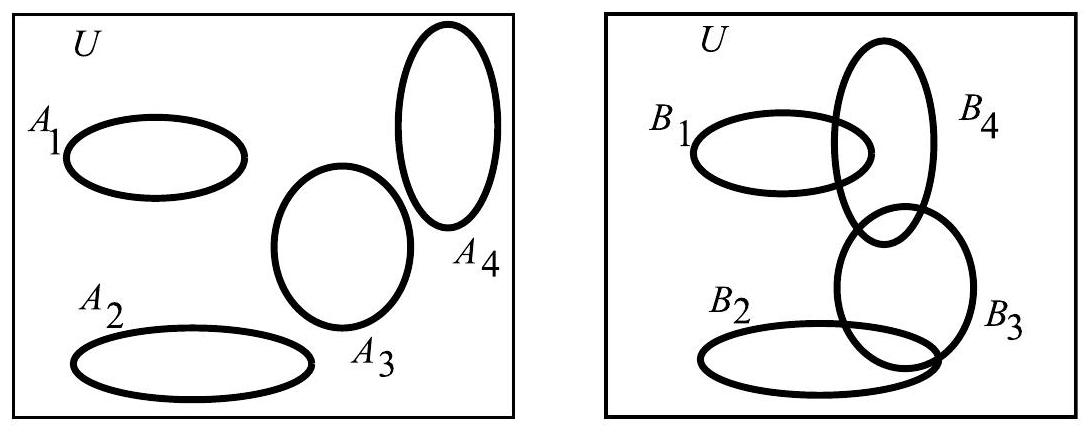
1. Is the family of sets $𝒜$ a disjoint family of sets? A pairwise disjoint family of sets?

2. Is the family of sets $ℬ$ a disjoint family of sets? A pairwise disjoint family of sets?

Now let the universal set be $ℝ$. For each $n\in \mathbb{N}$, let $C_n=(n,\mathrm{\infty })$, and let $𝒞=\{C_n\mid n\in \mathbb{N}\}$.

1. Is the family of sets $𝒞$ a disjoint family of sets? A pairwise disjoint family of sets?

5.5.11 Exercises for Section 5.5

1. For each natural number $n$, let $A_n=\{n,n+1,n+2,n+3\}$. Use the roster method to specify each of the following sets:

   1. $(\star )$ ${\bigcap }_{j=1}^3{A}_j$

   2. ${\bigcup }_{j=1}^3{A}_j$

   3. ${\bigcap }_{j=3}^7{A}_j$

   4. ${\bigcup }_{j=3}^7{A}_j$

   5. $A_9\cap \left({\bigcup }_{j=3}^7{A}_j\right)$

   6. ${\bigcup }_{j=3}^7\left(A_9\cap A_j\right)$

2. For each natural number $n$, let $A_n=\{k\in \mathbb{N}\mid k\ge n\}$. Assuming the universal set is $\mathbb{N}$, use the roster method or set builder notation to specify each of the following sets:

   1. $(\star )$ ${\bigcap }_{j=1}^5{A}_j$

   2. ${\left({\bigcap }_{j=1}^5{A}_j\right)}^c$

   3. $(\star )$ ${\bigcap }_{j=1}^5{A}_j^c$

   4. $(\star )$ ${\bigcup }_{j=1}^5{A}_j^c$

   5. ${\bigcup }_{j=1}^5{A}_j$

   6. $(\star )$ ${\left({\bigcup }_{j=1}^5{A}_j\right)}^c$

   7. ${\bigcap }_{j\in \mathbb{N}}{A}_j$

   8. ${\bigcup }_{j\in \mathbb{N}}{A}_j$

3. For each positive real number $r$, define $T_r$ to be the closed interval $[-r^2,r^2]$. That is,

   $$T_r=\{x\in ℝ\mid -r^2\le x\le r^2\}.$$

   Let $\mathrm{\Lambda }=\{m\in \mathbb{N}\mid 1\le m\le 10\}$. Use either interval notation or set builder notation to specify each of the following sets:

   1. $(\star )$ ${\bigcup }_{k\in \mathrm{\Lambda }}{T}_k$

   2. $(\star )$ ${\bigcap }_{k\in \mathrm{\Lambda }}{T}_k$

   3. ${\bigcup }_{r\in {ℝ}^{+}}{T}_r$

   4. ${\bigcap }_{r\in {ℝ}^{+}}{T}_r$

   5. ${\bigcup }_{k\in \mathbb{N}}{T}_k$

   6. ${\bigcap }_{k\in \mathbb{N}}{T}_k$

4. Prove Parts (2) and (4) of Theorem 5.30. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets.

   1. $(\star )$ For each $\beta \in \mathrm{\Lambda },A_{\beta }\subseteq {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$.

   2. ${\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$

5. Prove Theorem 5.31. Let $\mathrm{\Lambda }$ be a nonempty indexing set, let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets, and let $B$ be a set. Then

   1. $(\star )$ $B\cap \left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcup }_{\alpha \in \mathrm{\Lambda }}\left(B\cap A_{\alpha }\right)$, and

   2. $B\cup \left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcap }_{\alpha \in \mathrm{\Lambda }}\left(B\cup A_{\alpha }\right)$.

6. Let $\mathrm{\Lambda }$ and $\mathrm{\Gamma }$ be nonempty indexing sets. (Note: The letter $\mathrm{\Gamma }$ is the uppercase Greek letter gamma.) Also, let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ and $ℬ=\{B_{\beta }\mid \beta \in \mathrm{\Gamma }\}$ be indexed families of sets. Use the distributive laws in Exercise (5) to:

   1. Write $\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)\cap \left({\bigcup }_{\beta \in \mathrm{\Gamma }}{B}_{\beta }\right)$ as a union of intersections of two sets.

   2. Write $\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)\cup \left({\bigcap }_{\beta \in \mathrm{\Gamma }}{B}_{\beta }\right)$ as an intersection of unions of two sets.

7. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets. Also, assume that $\mathrm{\Gamma }\subseteq \mathrm{\Lambda }$ and $\mathrm{\Gamma }\ne \mathrm{\varnothing }$. Prove that

   1. ${\bigcup }_{\alpha \in \mathrm{\Gamma }}{A}_{\alpha }\subseteq {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$

   2. ${\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\subseteq {\bigcap }_{\alpha \in \mathrm{\Gamma }}{A}_{\alpha }$

8. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets.

   1. $(\star )$ Prove that if $B$ is a set such that $B\subseteq A_{\alpha }$ for every $\alpha \in \mathrm{\Lambda }$, then $B\subseteq {\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$.

   2. Prove that if $C$ is a set such that $A_{\alpha }\subseteq C$ for every $\alpha \in \mathrm{\Lambda }$, then ${\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\subseteq C$.

9. For each natural number $n$, let . Prove that $\{A_n\mid n\in \mathbb{N}\}$ is a pairwise disjoint family of sets and that ${\bigcup }_{n\in \mathbb{N}}{A}_n=\left({ℝ}^{+}-\mathbb{N}\right)$.

10. For each natural number $n$, let $A_n=\{k\in \mathbb{N}\mid k\ge n\}$. Determine if the following statements are true or false. Justify each conclusion.

    1. For all $j,k\in \mathbb{N}$, if $j\ne k$, then $A_j\cap A_k\ne \mathrm{\varnothing }$.

    2. ${\bigcap }_{k\in \mathbb{N}}{A}_k=\mathrm{\varnothing }$

11. Give an example of an indexed family of sets $\{A_n\mid n\in \mathbb{N}\}$ such all three of the following conditions are true:

    1. For each $m\in \mathbb{N},A_m\subseteq (0,1)$;

    2. For each $j,k\in \mathbb{N}$, if $j\ne k$, then $A_j\cap A_k\ne \mathrm{\varnothing }$; and

    3. ${\bigcap }_{k\in \mathbb{N}}{A}_k=\mathrm{\varnothing }$.

12. Let $\mathrm{\Lambda }$ be a nonempty indexing set, let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets, and let $B$ be a set. Use the results of Theorem 5.30 and Theorem 5.31 to prove each of the following:

    1. $(\star )$ $\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)-B={\bigcup }_{\alpha \in \mathrm{\Lambda }}\left(A_{\alpha }-B\right)$

    2. $\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)-B={\bigcap }_{\alpha \in \mathrm{\Lambda }}\left(A_{\alpha }-B\right)$

    3. $B-\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcap }_{\alpha \in \mathrm{\Lambda }}\left(B-A_{\alpha }\right)$

    4. $B-\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcup }_{\alpha \in \mathrm{\Lambda }}\left(B-A_{\alpha }\right)$

5.5.12 Explorations and Activities

1. An Indexed Family of Subsets of the Cartesian Plane. Let ${ℝ}^{\ast }$ be the set of nonnegative real numbers, and for each $r\in {ℝ}^{\ast }$, let

$C_r$ $=\{(x,y)\in ℝ\times ℝ\mid x^2+y^2=r^2\}$

$D_r$ $=\{(x,y)\in ℝ\times ℝ\mid x^2+y^2\le r^2\}$

$T_r$ $=\{(x,y)\in ℝ\times ℝ\mid x^2+y^2>r^2\}=D_r^c$

If $r>0$, then the set $C_r$ is the circle of radius $r$ with center at the origin as shown in Figure 5.8, and the set $D_r$ is the shaded disk (including the boundary) shown in Figure 5.8.

Figure 5.8: Two Sets for Activity 13

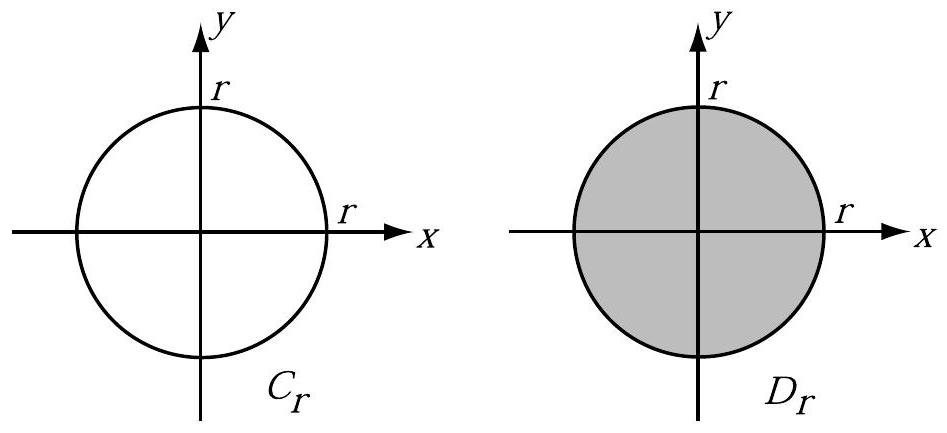
1. Determine ${\bigcup }_{r\in {ℝ}^{\ast }}{C}_r$ and ${\bigcap }_{r\in {ℝ}^{\ast }}{C}_r$.

2. Determine ${\bigcup }_{r\in {ℝ}^{\ast }}{D}_r$ and ${\bigcap }_{r\in {ℝ}^{\ast }}{D}_r$.

3. Determine ${\bigcup }_{r\in {ℝ}^{\ast }}{T}_r$ and ${\bigcap }_{r\in {ℝ}^{\ast }}{T}_r$.

4. Let $𝒞=\{C_r\mid r\in {ℝ}^{\ast }\},𝒟=\{D_r\mid r\in {ℝ}^{\ast }\}$, and $𝒯=\{T_r\mid r\in {ℝ}^{\ast }\}$. Are any of these indexed families of sets pairwise disjoint? Explain.

   Now let $I$ be the closed interval $[0,2]$ and let $J$ be the closed interval $[1,2]$.

5. Determine ${\bigcup }_{r\in I}{C}_r,{\bigcap }_{r\in I}{C}_r,{\bigcup }_{r\in J}{C}_r$, and ${\bigcap }_{r\in J}{C}_r$.

6. Determine ${\bigcup }_{r\in I}{D}_r,{\bigcap }_{r\in I}{D}_r,{\bigcup }_{r\in J}{D}_r$, and ${\bigcap }_{r\in J}{D}_r$.

7. Determine ${\left({\bigcup }_{r\in I}{D}_r\right)}^c,{\left({\bigcap }_{r\in I}{D}_r\right)}^c,{\left({\bigcup }_{r\in J}{D}_r\right)}^c$, and ${\left({\bigcap }_{r\in J}{D}_r\right)}^c$.

8. Determine ${\bigcup }_{r\in I}{T}_r,{\bigcap }_{r\in I}{T}_r,{\bigcup }_{r\in J}{T}_r$, and ${\bigcap }_{r\in J}{T}_r$.

9. Use De Morgan’s Laws to explain the relationship between your answers in Parts (13g) and (13h).

5.6 Chapter 5 Summary

5.6.1 Important Definitions

• Equal sets, Section 2.3

• Subset, Section 2.3

• Proper subset, Section 5.1

• Power set, Section 5.1

• Cardinality of a finite set, Section 5.1

• Intersection of two sets, Section 5.1

• Union of two sets, Section 5.1

• Set difference, Section 5.1

• Complement of a set, Section 5.1

• Disjoint sets, Section 5.2

• Cartesian product of two sets, Section 5.4

• Ordered pair, Section 5.4

• Union over a family of sets, Section 5.5

• Intersection over a family of sets, Section 5.5

• Indexing set, Section 5.5

• Indexed family of sets, Section 5.5

• Union over an indexed family of sets, Section 5.5

• Intersection over an indexed family of sets, Section 5.5

• Pairwise disjoint family of sets, Section 5.5

5.6.2 Important Theorems and Results about Sets

• Theorem 5.5. Let $n$ be a nonnegative integer and let $A$ be a subset of some universal set. If $A$ is a finite set with $n$ elements, then $A$ has $2^n$ subsets. That is, if $|A|=n$, then $|𝒫(A)|=2^n$.

• Theorem 5.18. Let $A,B$, and $C$ be subsets of some universal set $U$. Then all of the following equalities hold.

Properties of the Empty Set	$A\cap \mathrm{\varnothing }=\mathrm{\varnothing }$
and the Universal Set	$A\cup \mathrm{\varnothing }=A$
Idempotent Laws	$A\cap A=A$
Commutative Laws	$A\cap B=B\cap A$
Associative Laws	$(A\cap B)\cap C=A\cap (B\cap C)$
	$(A\cup B)\cup C=A\cup (B\cup C)$

Distributive Laws

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

• Theorem 5.20. Let $A$ and $B$ be subsets of some universal set $U$. Then the following are true:

Basic Properties	${\left(A^c\right)}^c=A$ $A-B=A\cap B^c$
Empty Set, Universal Set	$A-\mathrm{\varnothing }=A\text{ and }A-U=\mathrm{\varnothing }$ ${\mathrm{\varnothing }}^c=U\text{ and }{U}^c=\mathrm{\varnothing }$
De Morgan’s Laws	${(A\cap B)}^c=A^c\cup B^c$ ${(A\cup B)}^c=A^c\cap B^c$
Subsets and Complements	$A\subseteq B$ if and only if $B^c\subseteq A^c$.

• Theorem 5.25. Let $A,B$, and $C$ be sets. Then

1. $A\times (B\cap C)=(A\times B)\cap (A\times C)$

2. $A\times (B\cup C)=(A\times B)\cup (A\times C)$

3. $(A\cap B)\times C=(A\times C)\cap (B\times C)$

4. $(A\cup B)\times C=(A\times C)\cup (B\times C)$

5. $A\times (B-C)=(A\times B)-(A\times C)$

6. $(A-B)\times C=(A\times C)-(B\times C)$

7. If $T\subseteq A$, then $T\times B\subseteq A\times B$.

8. If $Y\subseteq B$, then $A\times Y\subseteq A\times B$.

• Theorem 5.30. Let $\mathrm{\Lambda }$ be a nonempty indexing set and let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets. Then

1. For each $\beta \in \mathrm{\Lambda },{\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\subseteq A_{\beta }$.

2. For each $\beta \in \mathrm{\Lambda },A_{\beta }\subseteq {\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }$.

3. ${\left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$

4. ${\left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)}^c={\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }^c$

Parts (3) and (4) are known as De Morgan’s Laws.

• Theorem 5.31. Let $\mathrm{\Lambda }$ be a nonempty indexing set, let $𝒜=\{A_{\alpha }\mid \alpha \in \mathrm{\Lambda }\}$ be an indexed family of sets, and let $B$ be a set. Then

1. $B\cap \left({\bigcup }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcup }_{\alpha \in \mathrm{\Lambda }}\left(B\cap A_{\alpha }\right)$, and

2. $B\cup \left({\bigcap }_{\alpha \in \mathrm{\Lambda }}{A}_{\alpha }\right)={\bigcap }_{\alpha \in \mathrm{\Lambda }}\left(B\cup A_{\alpha }\right)$.

5.6.3 Important Proof Method: The Choose-an-Element Method

The choose-an-element method is frequently used when we encounter a universal quantifier in a statement in the backward process of a proof. This statement often has the form

For each element with a given property, something happens.

In the forward process of the proof, we then we choose an arbitrary element with the given property.

Whenever we choose an arbitrary element with a given property, we are not selecting a specific element. Rather, the only thing we can assume about the element is the given property.