6 Functions

6.3 Injections, Surjections, and Bijections

Functions are frequently used in mathematics to define and describe certain relationships between sets and other mathematical objects. In addition, functions can be used to impose certain mathematical structures on sets. In this section, we will study special types of functions that are used to describe these relationships that are called injections and surjections. Before defining these types of functions, we will revisit what the definition of a function tells us and explore certain functions with finite domains.

6.3.1 Beginning Activity 1 (Functions with Finite Domains)

Let $A$ and $B$ be sets. Given a function $f:A\rightarrow B$ , we know the following:

•

For every $x\in A,f(x)\in B$ . That is, every element of $A$ is an input for the function $f$ . This could also be stated as follows: For each $x\in A$ , there exists a $y\in B$ such that $y=f(x)$ .
•

For a given $x\in A$ , there is exactly one $y\in B$ such that $y=f(x)$ .

The definition of a function does not require that different inputs produce different outputs. That is, it is possible to have $x_{1},x_{2}\in A$ with $x_{1}\neq x_{2}$ and $f\left(x_{1}\right)=f\left(x_{2}\right)$ . The arrow diagram for the function $f$ in Figure 6.5 illustrates such a function.

Also, the definition of a function does not require that the range of the function must equal the codomain. The range is always a subset of the codomain, but these two sets are not required to be equal. That is, if $g:A\rightarrow B$ , then it is possible to have a $y\in B$ such that $g(x)\neq y$ for all $x\in A$ . The arrow diagram for the function $g$ in Figure 6.5 illustrates such a function.

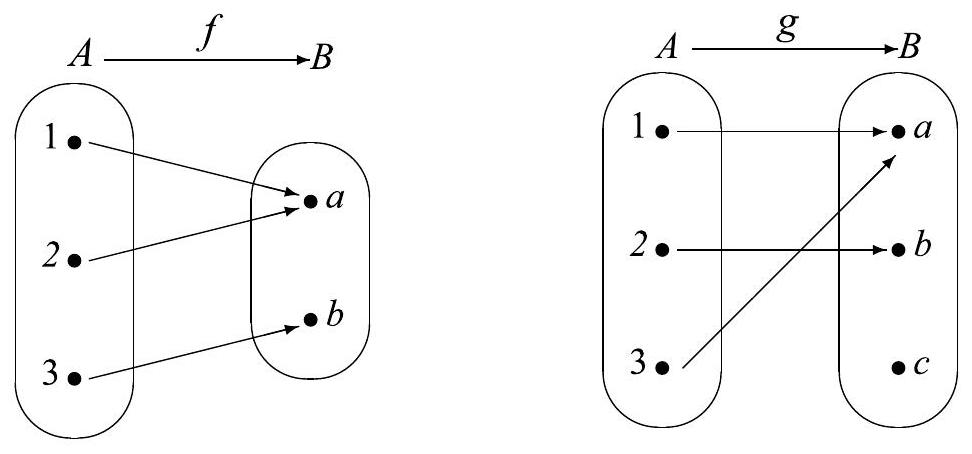
Two arrow diagrams. Diagram f maps 1, 2, 3 to a, b, c, d: 1 to a, 2 to a, 3 to b. Diagram g maps 1, 2, 3 to a, b, c, d: 1 to a, 2 to b, 3 to c (d is unmapped). — Figure 6.5: Arrow Diagram for Two Functions

Now let $A=\{1,2,3\},B=\{a,b,c,d\}$ , and $C=\{s,t\}$ . Define

•

$f:A\rightarrow B$ defined by $f(1)=a,f(2)=b,f(3)=c$ .
•

$g:A\rightarrow B$ defined by $g(1)=a,g(2)=b,g(3)=a$ .
•

$h:A\rightarrow C$ defined by $h(1)=s,h(2)=t,h(3)=s$ .

1.

Which of these functions satisfy the following property for a function $F$ ?

For all $x,y\in\operatorname{dom}(F)$ , if $x\neq y$ , then $F(x)\neq F(y)$ .
2.

Which of these functions satisfy the following property for a function $F$ ?

For all $x,y\in\operatorname{dom}(F)$ , if $F(x)=F(y)$ , then $x=y$ .
3.

Determine the range of each of these functions.
4.

Which of these functions have their range equal to their codomain?
5.

Which of the these functions satisfy the following property for a function $F$ ?

For all $y$ in the codomain of $F$ , there exists an $x\in\operatorname{dom}(F)$ such that $F(x)=y$ .

6.3.2 Beginning Activity 2 (Statements Involving Functions)

Let $A$ and $B$ be nonempty sets and let $f:A\rightarrow B$ . In Beginning Activity 1, we determined whether or not certain functions satisfied some specified properties. These properties were written in the form of statements, and we will now examine these statements in more detail.

1.

Consider the following statement:
For all $x,y\in A$ , if $x\neq y$ , then $f(x)\neq f(y)$ .
1. (a)
  
  Write the contrapositive of this conditional statement.
2. (b)
  
  Write the negation of this conditional statement.
2.

Now consider the statement:

For all $y\in B$ , there exists an $x\in A$ such that $f(x)=y$ .
Write the negation of this statement.
3.

Let $g:\mathbb{R}\rightarrow\mathbb{R}$ be defined by $g(x)=5x+3$ , for all $x\in\mathbb{R}$ . Complete the following proofs of the following propositions about the function $g$ .

Proposition 1. For all $a,b\in\mathbb{R}$ , if $g(a)=g(b)$ , then $a=b$ .
Proof. We let $a,b\in\mathbb{R}$ , and we assume that $g(a)=g(b)$ and will prove that $a=b$ . Since $g(a)=g(b)$ , we know that

$5a+3=5b+3$

(Now prove that in this situation, $a=b$ .)

Proposition 2. For all $b\in\mathbb{R}$ , there exists an $a\in\mathbb{R}$ such that $g(a)=b$ .
Proof. We let $b\in\mathbb{R}$ . We will prove that there exists an $a\in\mathbb{R}$ such that $g(a)=b$ by constructing such an $a$ in $\mathbb{R}$ . In order for this to happen, we need $g(a)=5a+3=b$ .
(Now solve the equation for $a$ and then show that for this real number $a$ , $g(a)=b$ .)

6.3.3 Injections

In previous sections and in Beginning Activity 1, we have seen examples of functions for which there exist different inputs that produce the same output. Using more formal notation, this means that there are functions $f:A\rightarrow B$ for which there exist $x_{1},x_{2}\in A$ with $x_{1}\neq x_{2}$ and $f\left(x_{1}\right)=f\left(x_{2}\right)$ . The work in the beginning activities was intended to motivate the following definition.
Definition. Let $f:A\rightarrow B$ be a function from the set $A$ to the set $B$ . The function $f$ is called an injection provided that

\text{ for all }x_{1},x_{2}\in A\text{, if }x_{1}\neq x_{2}\text{, then }f% \left(x_{1}\right)\neq f\left(x_{2}\right)\text{. }

When $f$ is an injection, we also say that $f$ is a one-to-one function, or that $f$ is an injective function.

Notice that the condition that specifies that a function $f$ is an injection is given in the form of a conditional statement. As we shall see, in proofs, it is usually easier to use the contrapositive of this conditional statement. Although we did not define the term then, we have already written the contrapositive for the conditional statement in the definition of an injection in Part (1) of Beginning Activity 2. In that activity, we also wrote the negation of the definition of an injection. Following is a summary of this work giving the conditions for $f$ being an injection or not being an injection.

Let $\boldsymbol{f}:\boldsymbol{A}\rightarrow\boldsymbol{B}$ .
"The function $\boldsymbol{f}$ is an injection" means that

•

For all $x_{1},x_{2}\in A$ , if $x_{1}\neq x_{2}$ , then $f\left(x_{1}\right)\neq f\left(x_{2}\right)$ ; or
•

For all $x_{1},x_{2}\in A$ , if $f\left(x_{1}\right)=f\left(x_{2}\right)$ , then $x_{1}=x_{2}$ . "The function $\boldsymbol{f}$ is not an injection" means that
•

There exist $x_{1},x_{2}\in A$ such that $x_{1}\neq x_{2}$ and $f\left(x_{1}\right)=f\left(x_{2}\right)$ .

6.3.4 Progress Check 6.10 (Working with the Definition of an Injection)

Now that we have defined what it means for a function to be an injection, we can see that in Part (3) of Beginning Activity 2, we proved that the function $g:\mathbb{R}\rightarrow\mathbb{R}$ is an injection, where $g(x)=5x+3$ for all $x\in\mathbb{R}$ . Use the definition (or its negation) to determine whether or not the following functions are injections.

1.

$k:A\rightarrow B$ , where $A=\{a,b,c\},B=\{1,2,3,4\}$ , and $k(a)=4,k(b)=1$ , and $k(c)=3$ .
2.

$f:A\rightarrow C$ , where $A=\{a,b,c\},C=\{1,2,3\}$ , and $f(a)=2,f(b)=3$ , and $f(c)=2$ .
3.

$F:\mathbb{Z}\rightarrow\mathbb{Z}$ defined by $F(m)=3m+2$ for all $m\in\mathbb{Z}$
4.

$h:\mathbb{R}\rightarrow\mathbb{R}$ defined by $h(x)=x^{2}-3x$ for all $x\in\mathbb{R}$
5.

$R_{5}=\{0,1,2,3,4\}$ and $s:R_{5}\rightarrow R_{5}$ defined by $s(x)=x^{3}(\bmod 5)$ for all $x\in R_{5}$ .

6.3.5 Surjections

In previous sections and in Beginning Activity 1, we have seen that there exist functions $f:A\rightarrow B$ for which range $(f)=B$ . This means that every element of $B$ is an output of the function $f$ for some input from the set $A$ . Using quantifiers, this means that for every $y\in B$ , there exists an $x\in A$ such that $f(x)=y$ . One of the objectives of the beginning activities was to motivate the following definition.

Definition. Let $f:A\rightarrow B$ be a function from the set $A$ to the set $B$ . The function $f$ is called a surjection provided that the range of $f$ equals the codomain of $f$ . This means that
for every $y\in B$ , there exists an $x\in A$ such that $f(x)=y$ .
When $f$ is a surjection, we also say that $f$ is an onto function or that $f$ maps $\boldsymbol{A}$ onto $\boldsymbol{B}$ . We also say that $f$ is a surjective function.

One of the conditions that specifies that a function $f$ is a surjection is given in the form of a universally quantified statement, which is the primary statement used in proving a function is (or is not) a surjection. Although we did not define the term then, we have already written the negation for the statement defining a surjection in Part (2) of Beginning Activity 2. We now summarize the conditions for $f$ being a surjection or not being a surjection.

Let $\boldsymbol{f}:\boldsymbol{A}\rightarrow\boldsymbol{B}$ .
"The function $\boldsymbol{f}$ is a surjection" means that

•

$\operatorname{range}(f)=\operatorname{codom}(f)=B$ ; or
•

For every $y\in B$ , there exists an $x\in A$ such that $f(x)=y$ .
"The function $\boldsymbol{f}$ is not a surjection" means that
•

range $(f)\neq\operatorname{codom}(f)$ ; or
•

There exists a $y\in B$ such that for all $x\in A,f(x)\neq y$ .

One other important type of function is when a function is both an injection and surjection. This type of function is called a bijection.

Definition. A bijection is a function that is both an injection and a surjection. If the function $f$ is a bijection, we also say that $f$ is one-to-one and onto and that $f$ is a bijective function.

6.3.6 Progress Check 6.11 (Working with the Definition of a Surjection)

Now that we have defined what it means for a function to be a surjection, we can see that in Part (3) of Beginning Activity 2, we proved that the function $g:\mathbb{R}\rightarrow\mathbb{R}$ is a surjection, where $g(x)=5x+3$ for all $x\in\mathbb{R}$ . Determine whether or not the following functions are surjections.

1.

$k:A\rightarrow B$ , where $A=\{a,b,c\},B=\{1,2,3,4\}$ , and $k(a)=4,k(b)=1$ , and $k(c)=3$ .
2.

$f:\mathbb{R}\rightarrow\mathbb{R}$ defined by $f(x)=3x+2$ for all $x\in\mathbb{R}$ .
3.

$F:\mathbb{Z}\rightarrow\mathbb{Z}$ defined by $F(m)=3m+2$ for all $m\in\mathbb{Z}$ .
4.

$s:R_{5}\rightarrow R_{5}$ defined by $s(x)=x^{3}(\bmod 5)$ for all $x\in R_{5}$ .

6.3.7 The Importance of the Domain and Codomain

The functions in the next two examples will illustrate why the domain and the codomain of a function are just as important as the rule defining the outputs of a function when we need to determine if the function is a surjection.

An Important Lesson. In Examples 6.12 and 6.13, the same mathematical formula was used to determine the outputs for the functions. However, one function was not a surjection and the other one was a surjection. This illustrates the important fact that whether a function is surjective depends not only on the formula that defines the output of the function but also on the domain and codomain of the function.

The next example will show that whether or not a function is an injection also depends on the domain of the function.

6.3.8 Example 6.14 (A Function that Is an Injection but Is Not a Surjection)

Let $\mathbb{Z}^{*}=\{x\in\mathbb{Z}\mid x\geq 0\}=\mathbb{N}\cup\{0\}$ . Define $g:\mathbb{Z}^{*}\rightarrow\mathbb{N}$ by $g(x)=x^{2}+1$ . (Notice that this is the same formula used in Examples 6.12 and 6.13.) Following is a table of values for some inputs for the function $g$ .

$x$	$g(x)$
0	1
1	2
2	5
3	10
4	17
5	26

Notice that the codomain is $\mathbb{N}$ , and the table of values suggests that some natural numbers are not outputs of this function. So it appears that the function $g$ is not a surjection.

To prove that $g$ is not a surjection, pick an element of $\mathbb{N}$ that does not appear to be in the range. We will use 3, and we will use a proof by contradiction to prove that there is no $x$ in the domain ( $\mathbb{Z}^{*}$ ) such that $g(x)=3$ . So we assume that there exists an $x\in\mathbb{Z}^{*}$ with $g(x)=3$ . Then

\displaystyle x^{2}+1

\displaystyle=3

\displaystyle x^{2}

\displaystyle=2

\displaystyle x

\displaystyle=\pm\sqrt{2}.

But this is not possible since $\sqrt{2}\notin\mathbb{Z}^{*}$ . Therefore, there is no $x\in\mathbb{Z}^{*}$ with $g(x)=3$ . This means that for every $x\in\mathbb{Z}^{*},g(x)\neq 3$ . Therefore, 3 is not in the range of $g$ , and hence $g$ is not a surjection.

The table of values suggests that different inputs produce different outputs, and hence that $g$ is an injection. To prove that $g$ is an injection, assume that $s,t\in\mathbb{Z}^{*}$
(the domain) with $g(s)=g(t)$ . Then

\displaystyle s^{2}+1

\displaystyle=t^{2}+1

\displaystyle s^{2}

\displaystyle=t^{2}

Since $s,t\in\mathbb{Z}^{*}$ , we know that $s\geq 0$ and $t\geq 0$ . So the preceding equation implies that $s=t$ . Hence, $g$ is an injection.

An Important Lesson. The functions in the three preceding examples all used the same formula to determine the outputs. The functions in Examples 6.12 and 6.13 are not injections but the function in Example 6.14 is an injection. This illustrates the important fact that whether a function is injective not only depends on the formula that defines the output of the function but also on the domain of the function.

6.3.9 Progress Check 6.15 (The Importance of the Domain and Codomain)

Let $\mathbb{R}^{+}=\{y\in\mathbb{R}\mid y>0\}$ . Define

\displaystyle f:\mathbb{R}\rightarrow\mathbb{R}\text{ by }f(x)=e^{-x},\text{ % for each }x\in\mathbb{R},\text{ and }

\displaystyle g:\mathbb{R}\rightarrow\mathbb{R}^{+}\text{by }g(x)=e^{-x},\text% { for each }x\in\mathbb{R}

Determine if each of these functions is an injection or a surjection. Justify your conclusions. Note: Before writing proofs, it might be helpful to draw the graph of $y=e^{-x}$ . A reasonable graph can be obtained using $-3\leq x\leq 3$ and $-2\leq y\leq 10$ . Please keep in mind that the graph does not prove any conclusion, but may help us arrive at the correct conclusions, which will still need proof.

6.3.10 Working with a Function of Two Variables

It takes time and practice to become efficient at working with the formal definitions of injection and surjection. As we have seen, all parts of a function are important (the domain, the codomain, and the rule for determining outputs). This is especially true for functions of two variables.

For example, we define $f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\times\mathbb{R}$ by

f(a,b)=(2a+b,a-b)\text{ for all }(a,b)\in\mathbb{R}\times\mathbb{R}

Notice that both the domain and the codomain of this function are the set $\mathbb{R}\times\mathbb{R}$ . Thus, the inputs and the outputs of this function are ordered pairs of real numbers. For example,

f(1,1)=(3,0)\quad\text{ and }\quad f(-1,2)=(0,-3)

To explore whether or not $f$ is an injection, we assume that $(a,b)\in\mathbb{R}\times\mathbb{R}$ , $(c,d)\in\mathbb{R}\times\mathbb{R}$ , and $f(a,b)=f(c,d)$ . This means that

(2a+b,a-b)=(2c+d,c-d)

Since this equation is an equality of ordered pairs, we see that

\displaystyle 2a+b

\displaystyle=2c+d,\text{ and }

\displaystyle a-b

\displaystyle=c-d

By adding the corresponding sides of the two equations in this system, we obtain $3a=3c$ and hence, $a=c$ . Substituting $a=c$ into either equation in the system give us $b=d$ . Since $a=c$ and $b=d$ , we conclude that

(a,b)=(c,d)

Hence, we have shown that if $f(a,b)=f(c,d)$ , then $(a,b)=(c,d)$ . Therefore, $f$ is an injection.

Now, to determine if $f$ is a surjection, we let $(r,s)\in\mathbb{R}\times\mathbb{R}$ , where $(r,s)$ is considered to be an arbitrary element of the codomain of the function $f$ . Can we find an ordered pair $(a,b)\in\mathbb{R}\times\mathbb{R}$ such that $f(a,b)=(r,s)$ ? Working backward, we see that in order to do this, we need

(2a+b,a-b)=(r,s)

That is, we need

2a+b=r\quad\text{ and }\quad a-b=s.

Solving this system for $a$ and $b$ yields

a=\frac{r+s}{3}\text{ and }b=\frac{r-2s}{3}

Since $r,s\in\mathbb{R}$ , we can conclude that $a\in\mathbb{R}$ and $b\in\mathbb{R}$ and hence that $(a,b)\in\mathbb{R}\times\mathbb{R}$ .

We now need to verify that for these values of $a$ and $b$ , we get $f(a,b)=(r,s)$ . So

\displaystyle f(a,b)

\displaystyle=f\left(\frac{r+s}{3},\frac{r-2s}{3}\right)

\displaystyle=\left(2\left(\frac{r+s}{3}\right)+\frac{r-2s}{3},\frac{r+s}{3}-% \frac{r-2s}{3}\right)

\displaystyle=\left(\frac{2r+2s+r-2s}{3},\frac{r+s-r+2s}{3}\right)

\displaystyle=(r,s)

This proves that for all $(r,s)\in\mathbb{R}\times\mathbb{R}$ , there exists $(a,b)\in\mathbb{R}\times\mathbb{R}$ such that $f(a,b)=(r,s)$ . Hence, the function $f$ is a surjection. Since $f$ is both an injection and a surjection, it is a bijection.

6.3.11 Progress Check 6.16 (A Function of Two Variables)

Let $g:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}$ be defined by $g(x,y)=2x+y$ , for all $(x,y)\in\mathbb{R}\times\mathbb{R}$ .
Note: Be careful! One major difference between this function and the previous example is that for the function $g$ , the codomain is $\mathbb{R}$ , not $\mathbb{R}\times\mathbb{R}$ . It is a good idea to begin by computing several outputs for several inputs (and remember that the inputs are ordered pairs).

1.

Notice that the ordered pair $(1,0)\in\mathbb{R}\times\mathbb{R}$ . That is, $(1,0)$ is in the domain of $g$ . Also notice that $g(1,0)=2$ . Is it possible to find another ordered pair $(a,b)\in\mathbb{R}\times\mathbb{R}$ such that $g(a,b)=2$ ?
2.

Let $z\in\mathbb{R}$ . Then $(0,z)\in\mathbb{R}\times\mathbb{R}$ and so $(0,z)\in\operatorname{dom}(g)$ . Now determine $g(0,z)$ .
3.

Is the function $g$ an injection? Is the function $g$ a surjection? Justify your conclusions.

6.3.12 Exercises 6.3

1.
1. (a)
  
  Draw an arrow diagram that represents a function that is an injection but is not a surjection.
2. (b)
  
  Draw an arrow diagram that represents a function that is an injection and is a surjection.
3. (c)
  
  Draw an arrow diagram that represents a function that is not an injection and is not a surjection.
4. (d)
  
  Draw an arrow diagram that represents a function that is not an injection but is a surjection.
5. (e)
  
  Draw an arrow diagram that represents a function that is not a bijection.
2.
We know $R_{5}=\{0,1,2,3,4\}$ and $R_{6}=\{0,1,2,3,4,5\}$ . For each of the following functions, determine if the function is an injection and determine if the function is a surjection. Justify all conclusions.
1. (a)
  
  $(\star)$ $f:R_{5}\rightarrow R_{5}$ by $f(x)=x^{2}+4(\bmod 5)$ , for all $x\in R_{5}$
2. (b)
  
  $g:R_{6}\rightarrow R_{6}$ by $g(x)=x^{2}+4(\bmod 6)$ , for all $x\in R_{6}$
3. (c)
  
  $F:R_{5}\rightarrow R_{5}$ by $F(x)=x^{3}+4(\bmod 5)$ , for all $x\in R_{5}$
3.
For each of the following functions, determine if the function is an injection and determine if the function is a surjection. Justify all conclusions.
1. (a)
  
  $(\star)$ $f:\mathbb{Z}\rightarrow\mathbb{Z}$ defined by $f(x)=3x+1$ , for all $x\in\mathbb{Z}$ .
2. (b)
  
  $F:\mathbb{Q}\rightarrow\mathbb{Q}$ defined by $F(x)=3x+1$ , for all $x\in\mathbb{Q}$ .
3. (c)
  
  $g:\mathbb{R}\rightarrow\mathbb{R}$ defined by $g(x)=x^{3}$ , for all $x\in\mathbb{R}$ .
4. (d)
  
  $G:\mathbb{Q}\rightarrow\mathbb{Q}$ defined by $G(x)=x^{3}$ , for all $x\in\mathbb{Q}$ .
5. (e)
  
  $k:\mathbb{R}\rightarrow\mathbb{R}$ defined by $k(x)=e^{-x^{2}}$ , for all $x\in\mathbb{R}$ .
6. (f)
  
  $K:\mathbb{R}^{*}\rightarrow\mathbb{R}$ defined by $K(x)=e^{-x^{2}}$ , for all $x\in\mathbb{R}^{*}$ .
  
  Note: $\mathbb{R}^{*}=\{x\in\mathbb{R}\mid x\geq 0\}$ .
7. (g)
  
  $K_{1}:\mathbb{R}^{*}\rightarrow T$ defined by $K_{1}(x)=e^{-x^{2}}$ , for all $x\in\mathbb{R}^{*}$ , where $T=\{y\in\mathbb{R}\mid 0<y\leq 1\}$ .
8. (h)
  
  $(\star)$ $h:\mathbb{R}\rightarrow\mathbb{R}$ defined by $h(x)=\frac{2x}{x^{2}+4}$ , for all $x\in\mathbb{R}$ .
9. (i)
  
  $H:\{x\in\mathbb{R}\mid x\geq 0\}\rightarrow\left\{y\in\mathbb{R}\mid\,0\leq y% \leq\frac{1}{2}\right\}$ defined by $H(x)=\frac{2x}{x^{2}+4}$ , for all $x\in\{x\in\mathbb{R}\mid x\geq 0\}$ .
4.
For each of the following functions, determine if the function is a bijection. Justify all conclusions.
1. (a)
  
  $(\star)$ $F:\mathbb{R}\rightarrow\mathbb{R}$ defined by $F(x)=5x+3$ , for all $x\in\mathbb{R}$ .
2. (b)
  
  $(\star)$ $G:\mathbb{Z}\rightarrow\mathbb{Z}$ defined by $G(x)=5x+3$ , for all $x\in\mathbb{Z}$ .
3. (c)
  
  $f:(\mathbb{R}-\{4\})\rightarrow\mathbb{R}$ defined by $f(x)=\frac{3x}{x-4}$ , for all $x\in(\mathbb{R}-\{4\})$ .
4. (d)
  
  $g:(\mathbb{R}-\{4\})\rightarrow(\mathbb{R}-\{3\})$ defined by $g(x)=\frac{3x}{x-4}$ , for all $x\in(\mathbb{R}-\{4\})$ .
5.

Let $s:\mathbb{N}\rightarrow\mathbb{N}$ , where for each $n\in\mathbb{N},s(n)$ is the sum of the distinct natural number divisors of $n$ . This is the sum of the divisors function that was introduced in Beginning Activity 2 from Section 6.1. Is $s$ an injection? Is $s$ a surjection? Justify your conclusions.
6.

Let $d:\mathbb{N}\rightarrow\mathbb{N}$ , where $d(n)$ is the number of natural number divisors of $n$ . This is the number of divisors function introduced in Exercise (6) from Section 6.1.. Is the function $d$ an injection? Is the function $d$ a surjection? Justify your conclusions.
7.

$(\star)$ In Beginning Activity 2 from Section 6.1., we introduced the birthday function. Is the birthday function an injection? Is it a surjection? Justify your conclusions.
8.
1. (a)
  
  Let $f:\mathbb{Z}\times\mathbb{Z}\rightarrow\mathbb{Z}$ be defined by $f(m,n)=2m+n$ . Is the function $f$ an injection? Is the function $f$ a surjection? Justify your conclusions.
2. (b)
  
  Let $g:\mathbb{Z}\times\mathbb{Z}\rightarrow\mathbb{Z}$ be defined by $g(m,n)=6m+3n$ . Is the function $g$ an injection? Is the function $g$ a surjection? Justify your conclusions.
9.
$(\star)$
1. (a)
  
  Let $f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\times\mathbb{R}$ be defined by $f(x,y)=(2x,x+y)$ . Is the function $f$ an injection? Is the function $f$ a surjection? Justify your conclusions.
2. (b)
  
  Let $g:\mathbb{Z}\times\mathbb{Z}\rightarrow\mathbb{Z}\times\mathbb{Z}$ be defined by $g(x,y)=(2x,x+y)$ . Is the function $g$ an injection? Is the function $g$ a surjection? Justify your conclusions.
10.

Let $f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}$ be the function defined by $f(x,y)=-x^{2}y+3y$ , for all $(x,y)\in\mathbb{R}\times\mathbb{R}$ . Is the function $f$ an injection? Is the function $f$ a surjection? Justify your conclusions.
11.

Let $g:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}$ be the function defined by $g(x,y)=\left(x^{3}+2\right)\sin y$ , for all $(x,y)\in\mathbb{R}\times\mathbb{R}$ . Is the function $g$ an injection? Is the function $g$ a surjection? Justify your conclusions.
12.

Let $A$ be a nonempty set. The identity function on the set $\boldsymbol{A}$ , denoted by $I_{A}$ , is the function $I_{A}:A\rightarrow A$ defined by $I_{A}(x)=x$ for every $x$ in $A$ . Is $I_{A}$ an injection? Is $I_{A}$ a surjection? Justify your conclusions.
13.

Let $A$ and $B$ be two nonempty sets. Define

$p_{1}:A\times B\rightarrow A\text{ by }p_{1}(a,b)=a$
for every $(a,b)\in A\times B$ . This is the first projection function introduced in Exercise (5) in Section 6.2..
1. (a)
  
  Is the function $p_{1}$ a surjection? Justify your conclusion.
2. (b)
  
  If $B=\{b\}$ , is the function $p_{1}$ an injection? Justify your conclusion.
3. (c)
  
  Under what condition(s) is the function $p_{1}$ not an injection? Make a conjecture and prove it.
14.

Define $f:\mathbb{N}\rightarrow\mathbb{Z}$ as follows: For each $n\in\mathbb{N}$ ,

$f(n)=\frac{1+(-1)^{n}(2n-1)}{4}.$

Is the function $f$ an injection? Is the function $f$ a surjection? Justify your conclusions.

Suggestions. Start by calculating several outputs for the function before you attempt to write a proof. In exploring whether or not the function is an injection, it might be a good idea to use cases based on whether the inputs are even or odd. In exploring whether $f$ is a surjection, consider using cases based on whether the output is positive or less than or equal to zero.
15.

Let $C$ be the set of all real functions that are continuous on the closed interval $[0,1]$ . Define the function $A:C\rightarrow\mathbb{R}$ as follows: For each $f\in C$ ,

$A(f)=\int_{0}^{1}f(x)dx$

Is the function $A$ an injection? Is it a surjection? Justify your conclusions.
16.

Let $A=\{(m,n)\mid m\in\mathbb{Z},n\in\mathbb{Z}$ , and $n\neq 0\}$ . Define $f:A\rightarrow\mathbb{Q}$ as follows:

$\text{ For each }(m,n)\in A,f(m,n)=\frac{m+n}{n}\text{. }$
1. (a)
  
  Is the function $f$ an injection? Justify your conclusion.
2. (b)
  
  Is the function $f$ a surjection? Justify your conclusion.
17.
Evaluation of proofs. See the instructions for Exercise (19) from Section 3.1.
1. (a)
  
  Proposition. The function $f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\times\mathbb{R}$ defined by $f(x,y)=(2x+y,x-y)$ is an injection.
  
  Proof. For each $(a,b)$ and $(c,d)$ in $\mathbb{R}\times\mathbb{R}$ , if $f(a,b)=f(c,d)$ , then
  
  $(2a+b,a-b)=(2c+d,c-d)$
  
  We will use systems of equations to prove that $a=c$ and $b=d$ .
  
  $\displaystyle 2a+b$ $\displaystyle=2c+d$
  
  $\displaystyle a-b$ $\displaystyle=c-d$
  
  $\displaystyle 3a$ $\displaystyle=3c$
  
  $\displaystyle a$ $\displaystyle=c$
  
  Since $a=c$ , we see that
  
  $(2c+b,c-b)=(2c+d,c-d)$
  
  So $b=d$ . Therefore, we have proved that the function $f$ is an injection.
2. (b)
  
  Proposition. The function $f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\times\mathbb{R}$ defined by $f(x,y)=(2x+y,x-y)$ is a surjection.
  
  Proof. We need to find an ordered pair such that $f(x,y)=(a,b)$ for each $(a,b)$ in $\mathbb{R}\times\mathbb{R}$ . That is, we need $(2x+y,x-y)=(a,b)$ , or
  
  $2x+y=a\quad\text{ and }\quad x-y=b.$
  
  Treating these two equations as a system of equations and solving for $x$ and $y$ , we find that
  
  $x=\frac{a+b}{3}\quad\text{ and }\quad y=\frac{a-2b}{3}.$
  
  Hence, $x$ and $y$ are real numbers, $(x,y)\in\mathbb{R}\times\mathbb{R}$ , and
  
  $\displaystyle f(x,y)$ $\displaystyle=f\left(\frac{a+b}{3},\frac{a-2b}{3}\right)$
  
  $\displaystyle=\left(2\left(\frac{a+b}{3}\right)+\frac{a-2b}{3},\frac{a+b}{3}-% \frac{a-2b}{3}\right)$
  
  $\displaystyle=\left(\frac{2a+2b+a-2b}{3},\frac{a+b-a+2b}{3}\right)$
  
  $\displaystyle=\left(\frac{3a}{3},\frac{3b}{3}\right)$
  
  $\displaystyle=(a,b).$
  
  Therefore, we have proved that for every $(a,b)\in\mathbb{R}\times\mathbb{R}$ , there exists an $(x,y)\in\mathbb{R}\times\mathbb{R}$ such that $f(x,y)=(a,b)$ . This proves that the function $f$ is a surjection. $\square$

6.3.13 Explorations and Activities

18.

Piecewise Defined Functions. We often say that a function is a piecewise defined function if it has different rules for determining the output for different parts of its domain. For example, we can define a function $f:\mathbb{R}\rightarrow\mathbb{R}$ by giving a rule for calculating $f(x)$ when $x\geq 0$ and giving a rule for calculating $f(x)$ when $x<0$ as follows:

$f(x)=\begin{cases}x^{2}+1,&\text{ if }x\geq 0;\\ x-1&\text{ if }x<0.\end{cases}$
1. (a)
  
  Sketch a graph of the function $f$ . Is the function $f$ an injection? Is the function $f$ a surjection? Justify your conclusions.
  
  For each of the following functions, determine if the function is an injection and determine if the function is a surjection. Justify all conclusions.
2. (b)
  
  $g:[0,1]\rightarrow(0,1)$ by $g(x)=\begin{cases}0.8,&\text{ if }x=0;\\ 0.5x,&\text{ if }0<x<1;\\ 0.6&\text{ if }x=1.\end{cases}$
3. (c)
  
  $h:\mathbb{Z}\rightarrow\{0,1\}$ by $h(x)=\begin{cases}0,&\text{ if }x\text{ is even; }\\ 1,&\text{ if }x\text{ is odd. }\end{cases}$
19.
Functions Whose Domain is $\mathcal{M}_{2}(\mathbb{R})$ . Let $\mathcal{M}_{2}(\mathbb{R})$ represent the set of all 2 by 2 matrices over $\mathbb{R}$ .
1. (a)
  
  Define det: $\mathcal{M}_{2}(\mathbb{R})\rightarrow\mathbb{R}$ by
  
  $\operatorname{det}\left[\begin{array}[]{ll}a&b\\ c&d\end{array}\right]=ad-bc.$
  
  This is the determinant function introduced in Exercise (9) from Section 6.2.. Is the determinant function an injection? Is the determinant function a surjection? Justify your conclusions.
2. (b)
  
  Define tran: $\mathcal{M}_{2}(\mathbb{R})\rightarrow\mathcal{M}_{2}(\mathbb{R})$ by
  
  $\operatorname{tran}\left[\begin{array}[]{ll}a&b\\ c&d\end{array}\right]=A^{T}=\left[\begin{array}[]{ll}a&c\\ b&d\end{array}\right].$
  
  This is the transpose function introduced in Exercise (10) from Section 6.2.. Is the transpose function an injection? Is the transpose function a surjection? Justify your conclusions.
3. (c)
  
  Define $F:\mathcal{M}_{2}(\mathbb{R})\rightarrow\mathbb{R}$ by
  
  $F\left[\begin{array}[]{ll}a&b\\ c&d\end{array}\right]=a^{2}+d^{2}-b^{2}-c^{2}$
  
  Is the function $F$ an injection? Is the function $F$ a surjection? Justify your conclusions.