6 Functions

6.4 Composition of Functions

6.4.1 Beginning Activity 1 (Constructing a New Function)

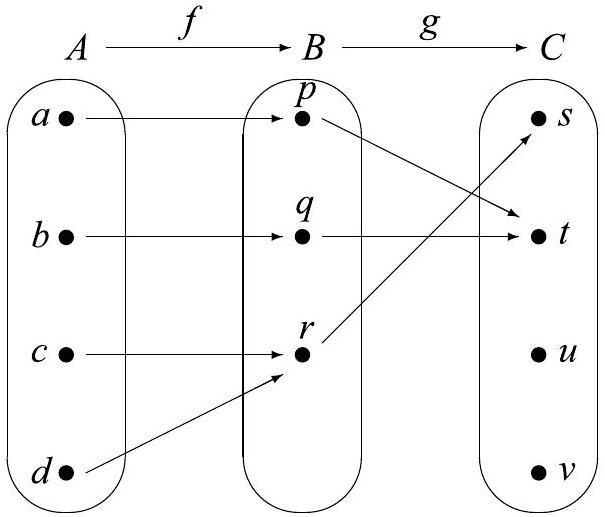
Let $A=\{a,b,c,d\},B=\{p,q,r\}$, and $C=\{s,t,u,v\}$. The arrow diagram in Figure 6.6 shows two functions: $f:A\to B$ and $g:B\to C$. Notice that if $x\in A$, then $f(x)\in B$. Since $f(x)\in B$, we can apply the function $g$ to $f(x)$, and we obtain $g(f(x))$, which is an element of $C$.

Using this process, determine $g(f(a)),g(f(b)),g(f(c))$, and $g(f(d))$. Then explain how we can use this information to define a function from $A$ to $C$.

Figure 6.6: Arrow Diagram Showing Two Functions

6.4.2 Beginning Activity 2 (Verbal Descriptions of Functions)

The outputs of most real functions we have studied in previous mathematics courses have been determined by mathematical expressions. In many cases, it is possible to use these expressions to give step-by-step verbal descriptions of how to compute the outputs. For example, if

$$f:ℝ\to ℝ\text{ is defined by }f(x)={(3x+2)}^3,$$

we could describe how to compute the outputs as follows:

Step	Verbal Description	Symbolic Result
1	Choose an input.	$x$
2	Multiply by 3.	$3x$
3	Add 2.	$3x+2$
4	Cube the result.	${(3x+2)}^3$

Complete step-by-step verbal descriptions for each of the following functions.

1. $f:ℝ\to ℝ$ by $f(x)=\sqrt{3x^2+2}$, for each $x\in ℝ$.

2. $g:ℝ\to ℝ$ by $g(x)=\sin \left(3x^2+2\right)$, for each $x\in ℝ$.

3. $h:ℝ\to ℝ$ by $h(x)=e^{3x^2+2}$, for each $x\in ℝ$.

4. $G:ℝ\to ℝ$ by $G(x)=\ln \left(x^4+3\right)$, for each $x\in ℝ$.

5. $k:ℝ\to ℝ$ by $k(x)=\sqrt[3]{\frac{\sin (4x+3)}{x^2+1}}$, for each $x\in ℝ$.

6.4.3 Composition of Functions

There are several ways to combine two existing functions to create a new function. For example, in calculus, we learned how to form the product and quotient of two functions and then how to use the product rule to determine the derivative of a product of two functions and the quotient rule to determine the derivative of the quotient of two functions.

The chain rule in calculus was used to determine the derivative of the composition of two functions, and in this section, we will focus only on the composition of two functions. We will then consider some results about the compositions of injections and surjections.

The basic idea of function composition is that when possible, the output of a function $f$ is used as the input of a function $g$. This can be referred to as "$f$ followed by $g$" and is called the composition of $f$ and $g$. In previous mathematics courses, we used this idea to determine a formula for the composition of two real functions.

For example, if

$$f(x)=3x^2+2\text{ and }g(x)=\sin x$$

then we can compute $g(f(x))$ as follows:

$g(f(x))$ $=g\left(3x^2+2\right)$

$=\sin \left(3x^2+2\right)$

In this case, $f(x)$, the output of the function $f$, was used as the input for the function $g$. We now give the formal definition of the composition of two functions.

Definition. Let $A,B$, and $C$ be nonempty sets, and let $f:A\to B$ and $g:B\to C$ be functions. The composition of $𝒇$ and $𝒈$ is the function $g\circ f:A\to C$ defined by

$$(g\circ f)(x)=g(f(x))$$

for all $x\in A$. We often refer to the function $g\circ f$ as a composite function.
It is helpful to think of the composite function $g\circ f$ as "$𝒇$ followed by $𝒈$." We then refer to $f$ as the inner function and $g$ as the outer function.

6.4.4 Composition and Arrow Diagrams

The concept of the composition of two functions can be illustrated with arrow diagrams when the domain and codomain of the functions are small, finite sets. Although the term "composition" was not used then, this was done in Beginning Activity 1, and another example is given here.

Let $A=\{a,b,c,d\},B=\{p,q,r\}$, and $C=\{s,t,u,v\}$. The arrow diagram in Figure 6.7 shows two functions: $f:A\to B$ and $g:B\to C$.

Figure 6.7: Arrow Diagram for Two Functions

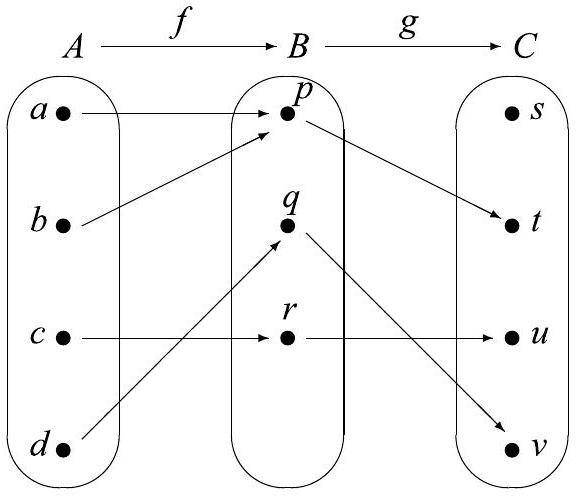
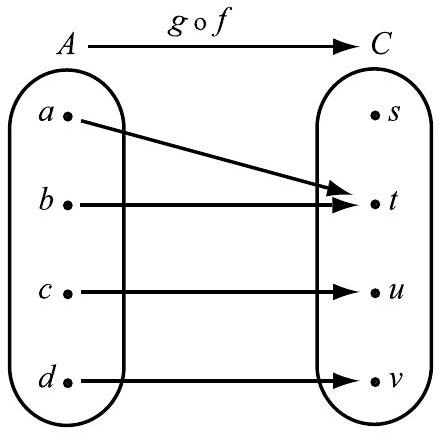
If we follow the arrows from the set $A$ to the set $C$, we will use the outputs of $f$ as inputs of $g$, and get the arrow diagram from $A$ to $C$ shown in Figure 6.8. This diagram represents the composition of $f$ followed by $g$.

Figure 6.8: Arrow Diagram for $g\circ f:A\to C$

6.4.5 Progress Check 6.17 (The Composition of Two Functions)

Let $A=\{a,b,c,d\}$ and $B=\{1,2,3\}$. Define the functions $f$ and $g$ as follows:

$f:A\to B\text{ defined by }f(a)=2,f(b)=3,f(c)=1,\text{ and }f(d)=2.$

$g:B\to B\text{ defined by }g(1)=3,g(2)=1,\text{ and }g(3)=2.$

Create arrow diagrams for the functions $f,g,g\circ f$, and $g\circ g$.

6.4.6 Decomposing Functions

We use the chain rule in calculus to find the derivative of a composite function. The first step in the process is to recognize a given function as a composite function. This can be done in many ways, but the work in Beginning Activity 2 can be used to decompose a function in a way that works well with the chain rule. The use of the terms "inner function" and "outer function" can also be helpful. The idea is that we use the last step in the process to represent the outer function, and the steps prior to that to represent the inner function. So for the function,

$$f:ℝ\to ℝ\text{ by }f(x)={(3x+2)}^3$$

the last step in the verbal description table was to cube the result. This means that we will use the function $g$ (the cubing function) as the outer function and will use the prior steps as the inner function. We will denote the inner function by $h$. So we let $h:ℝ\to ℝ$ by $h(x)=3x+2$ and $g:ℝ\to ℝ$ by $g(x)=x^3$. Then

$(g\circ h)(x)$ $=g(h(x))$

$=g(3x+2)$

$={(3x+2)}^3$

$=f(x).$

We see that $g\circ h=f$ and, hence, we have "decomposed" the function $f$. It should be noted that there are other ways to write the function $f$ as a composition of two functions, but the way just described is the one that works well with the chain rule. In this case, the chain rule gives

$f^{\prime }(x)$ $={(g\circ h)}^{\prime }(x)$

$=g^{\prime }(h(x))h^{\prime }(x)$

$=3{(h(x))}^2\cdot 3$

$=9{(3x+2)}^2$

6.4.7 Progress Check 6.18 (Decomposing Functions)

Write each of the following functions as the composition of two functions.

1. $F:ℝ\to ℝ$ by $F(x)={\left(x^2+3\right)}^3$

2. $G:ℝ\to ℝ$ by $G(x)=\ln \left(x^2+3\right)$

3. $f:\mathbb{Z}\to \mathbb{Z}$ by $f(x)=\left|x^2-3\right|$

4. $g:ℝ\to ℝ$ by $g(x)=\cos \left(\frac{2x-3}{x^2+1}\right)$

6.4.8 Theorems about Composite Functions

If $f:A\to B$ and $g:B\to C$, then we can form the composite function $g\circ f:A\to C$. In Section 6.3, we learned about injections and surjections. We now explore what type of function $g\circ f$ will be if the functions $f$ and $g$ are injections (or surjections).

6.4.9 Progress Check 6.19 (Compositions of Injections and Surjections)

Although other representations of functions can be used, it will be helpful to use arrow diagrams to represent the functions in this progress check. We will use the following sets:

$$A=\{a,b,c\},B=\{p,q,r\},C=\{u,v,w,x\},\text{ and }D=\{u,v\}.$$

1. Draw an arrow diagram for a function $f:A\to B$ that is an injection and an arrow diagram for a function $g:B\to C$ that is an injection. In this case, is the composite function $g\circ f:A\to C$ an injection? Explain.

2. Draw an arrow diagram for a function $f:A\to B$ that is a surjection and an arrow diagram for a function $g:B\to D$ that is a surjection. In this case, is the composite function $g\circ f:A\to D$ a surjection? Explain.

3. Draw an arrow diagram for a function $f:A\to B$ that is a bijection and an arrow diagram for a function $g:B\to A$ that is a bijection. In this case, is the composite function $g\circ f:A\to A$ bijection? Explain.

In Progress Check 6.19, we explored some properties of composite functions related to injections, surjections, and bijections. The following theorem contains
results that these explorations were intended to illustrate. Some of the proofs will be included in the exercises.

Theorem 6.20. Let $A,B$, and $C$ be nonempty sets and assume that $f:A\to B$ and $g:B\to C$.

1. If $f$ and $g$ are both injections, then ($g\circ f$): $A\to C$ is an injection.

2. If $f$ and $g$ are both surjections, then $(g\circ f):A\to C$ is a surjection.

3. If $f$ and $g$ are both bijections, then $(g\circ f):A\to C$ is a bijection.

The proof of Part (1) is Exercise (6). Part (3) is a direct consequence of the first two parts. We will discuss a process for constructing a proof of Part (2). Using the forward-backward process, we first look at the conclusion of the conditional statement in Part (2). The goal is to prove that $g\circ f$ is a surjection. Since $g\circ f:A\to C$, this is equivalent to proving that

For all $c\in C$, there exists an $a\in A$ such that $(g\circ f)(a)=c$.

Since this statement in the backward process uses a universal quantifier, we will use the choose-an-element method and choose an arbitrary element $c$ in the set $C$. The goal now is to find an $a\in A$ such that $(g\circ f)(a)=c$.

Now we can look at the hypotheses. In particular, we are assuming that both $f:A\to B$ and $g:B\to C$ are surjections. Since we have chosen $c\in C$, and $g:B\to C$ is a surjection, we know that
there exists a $b\in B$ such that $g(b)=c$.

Now, $b\in B$ and $f:A\to B$ is a surjection. Hence
there exists an $a\in A$ such that $f(a)=b$.

If we now compute $(g\circ f)(a)$, we will see that

$$(g\circ f)(a)=g(f(a))=g(b)=c$$

We can now write the proof as follows:

Proof of Theorem 6.20, Part (2). Let $A,B$, and $C$ be nonempty sets and assume that $f:A\to B$ and $g:B\to C$ are both surjections. We will prove that $g\circ f:A\to C$ is a surjection.

Let $c$ be an arbitrary element of $C$. We will prove there exists an $a\in A$ such that $(g\circ f)(a)=c$. Since $g:B\to C$ is a surjection, we conclude that
there exists a $b\in B$ such that $g(b)=c$.

Now, $b\in B$ and $f:A\to B$ is a surjection. Hence
there exists an $a\in A$ such that $f(a)=b$.

We now see that

$(g\circ f)(a)$ $=g(f(a))$

$=g(b)$

$=c.$

We have now shown that for every $c\in C$, there exists an $a\in A$ such that $(g\circ f)(a)=c$, and this proves that $g\circ f$ is a surjection.

Theorem 6.20 shows us that if $f$ and $g$ are both special types of functions, then the composition of $f$ followed by $g$ is also that type of function. The next question is, "If the composition of $f$ followed by $g$ is an injection (or surjection), can we make any conclusions about $f$ or $g$ ?" A partial answer to this question is provided in Theorem 6.21. This theorem will be investigated and proved in the Explorations and Activities for this section. See Exercise (10).

Theorem 6.21. Let $A,B$, and $C$ be nonempty sets and assume that $f:A\to B$ and $g:B\to C$.

1. If $g\circ f:A\to C$ is an injection, then $f:A\to B$ is an injection.

2. If $g\circ f:A\to C$ is a surjection, then $g:B\to C$ is a surjection.

6.4.10 Exercises 6.4

1. In our definition of the composition of two functions, $f$ and $g$, we required that the domain of $g$ be equal to the codomain of $f$. However, it is sometimes possible to form the composite function $g\circ f$ even though $\mathrm{dom}(g)\ne \mathrm{codom}(f)$. For example, let

   1. Is it possible to determine $(g\circ f)(x)$ for all $x\in ℝ$? Explain.

   2. In general, let $f:A\to T$ and $g:B\to C$. Find a condition on the domain of $g$ (other than $B=T$) that results in a meaningful definition of the composite function $g\circ f:A\to C$.

2. $(\star )$ Let $h:ℝ\to ℝ$ be defined by $h(x)=3x+2$ and $g:ℝ\to ℝ$ be defined by $g(x)=x^3$. Determine formulas for the composite functions $g\circ h$ and $h\circ g$. Is the function $g\circ h$ equal to the function $h\circ g$? Explain. What does this tell you about the operation of composition of functions?

3. $(\star )$ Following are formulas for certain real functions. Write each of these real functions as the composition of two functions. That is, decompose each of the functions.

   1. $F(x)=\cos \left(e^x\right)$

   2. $G(x)=e^{\cos (x)}$

   3. $H(x)=\frac{1}{\sin x}$

   4. $K(x)=\cos \left(e^{-x^2}\right)$

4. The identity function on a set $S$, denoted by $I_S$, is defined as follows: $I_S:S\to S$ by $I_S(x)=x$ for each $x\in S$. Let $f:A\to B$.

   1. $(\star )$ For each $x\in A$, determine $\left(f\circ I_A\right)(x)$ and use this to prove that $f\circ I_A=f$.

   2. Prove that $I_B\circ f=f$.

5. 1. $(\star )$ Let $f:ℝ\to ℝ$ be defined by $f(x)=x^2$, let $g:ℝ\to ℝ$ be defined by $g(x)=\sin x$, and let $h:ℝ\to ℝ$ be defined by $h(x)=\sqrt[3]{x}$.

      Determine formulas for $[(h\circ g)\circ f](x)$ and $[h\circ (g\circ f)](x)$. Does this prove that $(h\circ g)\circ f=h\circ (g\circ f)$ for these particular functions? Explain.

   2. Now let $A,B,C$, and $D$ be sets and let $f:A\to B,g:B\to C$, and $h:C\to D$. Prove that $(h\circ g)\circ f=h\circ (g\circ f)$. That is, prove that function composition is an associative operation.

6. $(\star )$ Prove Part (1) of Theorem 6.20. Let $A,B$, and $C$ be nonempty sets and let $f:A\to B$ and $g:B\to C$. If $f$ and $g$ are both injections, then $g\circ f$ is an injection.

7. For each of the following, give an example of functions $f:A\to B$ and $g:B\to C$ that satisfy the stated conditions, or explain why no such example exists.

   1. $(\star )$ The function $f$ is a surjection, but the function $g\circ f$ is not a surjection.

   2. $(\star )$ The function $f$ is an injection, but the function $g\circ f$ is not an injection.

   3. The function $g$ is a surjection, but the function $g\circ f$ is not a surjection.

   4. The function $g$ is an injection, but the function $g\circ f$ is not an injection.

   5. The function $f$ is not a surjection, but the function $g\circ f$ is a surjection.

   6. $(\star )$ The function $f$ is not an injection, but the function $g\circ f$ is an injection.

   7. The function $g$ is not a surjection, but the function $g\circ f$ is a surjection.

   8. The function $g$ is not an injection, but the function $g\circ f$ is an injection.

8. Let $A$ be a nonempty set and let $f:A\to A$. For each $n\in \mathbb{N}$, define a function $f^n:A\to A$ recursively as follows: $f^1=f$ and for each $n\in \mathbb{N}$, $f^{n+1}=f\circ f^n$. For example, $f^2=f\circ f^1=f\circ f$ and $f^3=f\circ f^2=f\circ (f\circ f)$.

   1. Let $f:ℝ\to ℝ$ by $f(x)=x+1$ for each $x\in ℝ$. For each $n\in \mathbb{N}$ and for each $x\in ℝ$, determine a formula for $f^n(x)$ and use induction to prove that your formula is correct.

   2. Let $a,b\in ℝ$ and let $f:ℝ\to ℝ$ by $f(x)=ax+b$ for each $x\in ℝ$. For each $n\in \mathbb{N}$ and for each $x\in ℝ$, determine a formula for $f^n(x)$ and use induction to prove that your formula is correct.

   3. Now let $A$ be a nonempty set and let $f:A\to A$. Use induction to prove that for each $n\in \mathbb{N},f^{n+1}=f^n\circ f$. (Note: You will need to use the result in Exercise (5).)

6.4.11 Explorations and Activities

1. Exploring Composite Functions. Let $A,B$, and $C$ be nonempty sets and let $f:A\to B$ and $g:B\to C$. For this activity, it may be useful to draw your arrow diagrams in a triangular arrangement as follows:

   

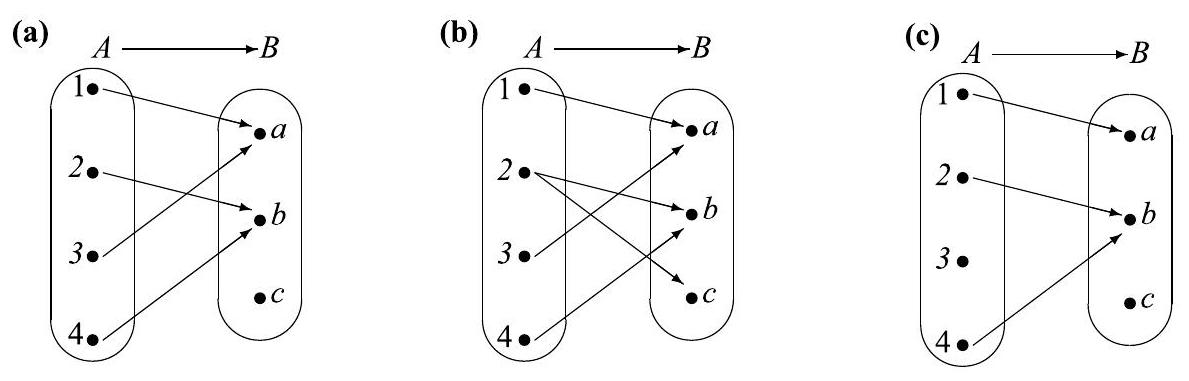
   It might be helpful to consider examples where the sets are small. Try constructing examples where the set $A$ has 2 elements, the set $B$ has 3 elements, and the set $C$ has 2 elements.

   1. Is it possible to construct an example where $g\circ f$ is an injection, $f$ is an injection, but $g$ is not an injection? Either construct such an example or explain why it is not possible.

   2. Is it possible to construct an example where $g\circ f$ is an injection, $g$ is an injection, but $f$ is not an injection? Either construct such an example or explain why it is not possible.

   3. Is it possible to construct an example where $g\circ f$ is a surjection, $f$ is a surjection, but $g$ is not a surjection? Either construct such an example or explain why it is not possible.

   4. Is it possible to construct an example where $g\circ f$ is surjection, $g$ is a surjection, but $f$ is not a surjection? Either construct such an example or explain why it is not possible.

2. The Proof of Theorem 6.21. Use the ideas from Exercise (9) to prove Theorem 6.21. Let $A,B$, and $C$ be nonempty sets and let $f:A\to B$ and $g:B\to C$.

   1. If $g\circ f:A\to C$ is an injection, then $f:A\to B$ is an injection.

   2. If $g\circ f:A\to C$ is a surjection, then $g:B\to C$ is a surjection.

      Hint: For part (a), start by asking, "What do we have to do to prove that $f$ is an injection?" Start with a similar question for part (b).