6 Functions

6.5 Inverse Functions

For this section, we will use the concept of Cartesian product of two sets $A$ and $B$, denoted by $A\times B$, which is the set of all ordered pairs ($x,y$) where $x\in A$ and $y\in B$. That is,

$$A\times B=\{(x,y)\mid x\in A\text{ and }y\in B\}.$$

See Beginning Activity 2 in Section 5.4 for a more thorough discussion of this concept.

6.5.1 Beginning Activity 1 (Functions and Sets of Ordered Pairs)

When we graph a real function, we plot ordered pairs in the Cartesian plane where the first coordinate is the input of the function and the second coordinate is the output of the function. For example, if $g:ℝ\to ℝ$, then every point on the graph of $g$ is an ordered pair $(x,y)$ of real numbers where $y=g(x)$. This shows how we can generate ordered pairs from a function. It happens that we can do this with any function. For example, let

$$A=\{1,2,3\}\text{ and }B=\{a,b\}$$

Define the function $F:A\to B$ by

$$F(1)=a,F(2)=b,\text{ and }F(3)=b.$$

We can convert each of these to an ordered pair in $A\times B$ by using the input as the first coordinate and the output as the second coordinate. For example, $F(1)=a$ is converted to $(1,a),F(2)=b$ is converted to $(2,b)$, and $F(3)=b$ is converted to $(3,b)$. So we can think of this function as a set of ordered pairs, which is a subset of $A\times B$, and write

$$F=\{(1,a),(2,b),(3,b)\}$$

Note: Since $F$ is the name of the function, it is customary to use $F$ as the name for the set of ordered pairs.

1. Let $A=\{1,2,3\}$ and let $C=\{a,b,c,d\}$. Define the function $g:A\to C$ by $g(1)=a,g(2)=b$, and $g(3)=d$. Write the function $g$ as a set of ordered pairs in $A\times C$.

   For another example, if we have a real function, such as $g:ℝ\to ℝ$ by $g(x)=x^2-2$, then we can think of $g$ as the following infinite subset of $ℝ\times ℝ$ :

   $$g=\{(x,y)\in ℝ\times ℝ\mid y=x^2-2\}$$

   We can also write this as $g=\{(x,x^2-2)\mid x\in ℝ\}$.

2. Let $f:\mathbb{Z}\to \mathbb{Z}$ be defined by $f(m)=3m+5$, for all $m\in \mathbb{Z}$. Use set builder notation to write the function $f$ as a set of ordered pairs, and then use the roster method to write the function $f$ as a set of ordered pairs.

   So any function $f:A\to B$ can be thought of as a set of ordered pairs that is a subset of $A\times B$. This subset is

   $$f=\{(a,f(a))\mid a\in A\}\text{ or }f=\{(a,b)\in A\times B\mid b=f(a)\}.$$

   On the other hand, if we started with $A=\{1,2,3\},B=\{a,b\}$, and

   $$G=\{(1,a),(2,a),(3,b)\}\subseteq A\times B$$

   then we could think of $G$ as a function from $A$ to $B$ with $G(1)=a,G(2)=a$, and $G(3)=b$. The idea is to use the first coordinate of each ordered pair as the input, and the second coordinate as the output. However, not every subset of $A\times B$ can be used to define a function from $A$ to $B$. This is explored in the following questions.

3. Let $f=\{(1,a),(2,a),(3,a),(1,b)\}$. Could this set of ordered pairs be used to define a function from $A$ to $B$? Explain.

4. Let $g=\{(1,a),(2,b),(3,a)\}$. Could this set of ordered pairs be used to define a function from $A$ to $B$? Explain.

5. Let $h=\{(1,a),(2,b)\}$. Could this set of ordered pairs be used to define a function from $A$ to $B$? Explain.

6.5.2 Beginning Activity 2 (A Composition of Two Specific Functions)

Let $A=\{a,b,c,d\}$ and let $B=\{p,q,r,s\}$.

1. Construct an example of a function $f:A\to B$ that is a bijection. Draw an arrow diagram for this function.

2. On your arrow diagram, draw an arrow from each element of $B$ back to its corresponding element in $A$. Explain why this defines a function from $B$ to A.

3. If the name of the function in Part (2) is $g$, so that $g:B\to A$, what are $g(p)$, $g(q),g(r)$, and $g(s)\mathrm{?}$

4. Construct a table of values for each of the functions $g\circ f:A\to A$ and $f\circ g:B\to B$. What do you observe about these tables of values?

6.5.3 The Ordered Pair Representation of a Function

In Beginning Activity 1, we observed that if we have a function $f:A\to B$, we can generate a set of ordered pairs $f$ that is a subset of $A\times B$ as follows:

$$f=\{(a,f(a))\mid a\in A\}\text{ or }f=\{(a,b)\in A\times B\mid b=f(a)\}.$$

However, we also learned that some sets of ordered pairs cannot be used to define a function. We now wish to explore under what conditions a set of ordered pairs can be used to define a function. Starting with a function $f:A\to B$, since $\mathrm{dom}(f)=A$, we know that

$$\text{ For every }a\in A\text{, there exists a }b\in B\text{ such that }(a,b)\in f\text{. }$$ (1)

Specifically, we use $b=f(a)$. This says that every element of $A$ can be used as an input. In addition, to be a function, each input can produce only one output. In terms of ordered pairs, this means that there will never be two ordered pairs $(a,b)$ and ($a,c$) in the function $f$ where $a\in A,b,c\in B$, and $b\ne c$. We can formulate this as a conditional statement as follows:

$\text{For every }a\in A\text{ and every }b,c\in B\text{,}$

$\text{if }(a,b)\in f\text{ and }(a,c)\in f\text{, then }b=c\text{.}$ (2)

This also means that if we start with a subset $f$ of $A\times B$ that satisfies conditions (1) and (2), then we can consider $f$ to be a function from $A$ to $B$ by using $b=f(a)$ whenever $(a,b)$ is in $f$. This proves the following theorem.

Theorem 6.22. Let $A$ and $B$ be nonempty sets and let $f$ be a subset of $A\times B$ that satisfies the following two properties:

• For every $a\in A$, there exists $b\in B$ such that $(a,b)\in f$; and

• For every $a\in A$ and every $b,c\in B$, if $(a,b)\in f$ and $(a,c)\in f$, then $b=c$.

If we use $f(a)=b$ whenever $(a,b)\in f$, then $f$ is a function from $A$ to $B$.

A Note about Theorem 6.22. The first condition in Theorem 6.22 means that every element of $A$ is an input, and the second condition ensures that every input has exactly one output. Many texts will use Theorem 6.22 as the definition of a function. Many mathematicians believe that this ordered pair representation of a function is the most rigorous definition of a function. It allows us to use set theory to work with and compare functions. For example, equality of functions becomes a question of equality of sets. Therefore, many textbooks will use the ordered pair representation of a function as the definition of a function.

6.5.4 Progress Check 6.23 (Sets of Ordered Pairs that Are Not Functions)

Let $A=\{1,2,3\}$ and let $B=\{a,b,c\}$. Explain why each of the following subsets of $A\times B$ cannot be used to define a function from $A$ to $B$.

1. $F=\{(1,a),(2,a)\}$.

2. $G=\{(1,a),(2,b),(3,c),(2,c)\}$.

6.5.5 The Inverse of a Function

In previous mathematics courses, we learned that the exponential function (with base $e$) and the natural logarithm function are inverses of each other. This was often expressed as follows:

For each $x\in ℝ$ with $x>0$ and for each $y\in ℝ$, $y=\ln x$ if and only if $x=e^y$.

Notice that this means that $x$ is the input and $y$ is the output for the natural logarithm function if and only if $y$ is the input and $x$ is the output for the exponential function. In essence, the inverse function (in this case, the exponential function) reverses the action of the original function (in this case, the natural logarithm function). In terms of ordered pairs (input-output pairs), this means that if $(x,y)$ is an ordered pair for a function, then $(y,x)$ is an ordered pair for its inverse. This idea of reversing the roles of the first and second coordinates is the basis for our definition of the inverse of a function.

Definition. Let $f:A\to B$ be a function. The inverse of $𝒇$, denoted by $f^{-1}$, is the set of ordered pairs $\{(b,a)\in B\times A\mid f(a)=b\}$. That is,

$$f^{-1}=\{(b,a)\in B\times A\mid f(a)=b\}.$$

If we use the ordered pair representation for $f$, we could also write

$$f^{-1}=\{(b,a)\in B\times A\mid (a,b)\in f\}.$$

Notice that this definition does not state that $f^{-1}$ is a function. It is simply a subset of $B\times A$. After we study the material in Chapter 7, we will say that this means that $f^{-1}$ is a relation from $B$ to $A$. This fact, however, is not important to us now. We are mainly interested in the following question:

6.5.6 Progress Check 6.24 (Exploring the Inverse of a Function)

Let $A=\{a,b,c\},B=\{a,b,c,d\}$, and $C=\{p,q,r\}$. Define

$f:A\to C$ by	$f(a)=r$	$f(b)=p$	$f(c)=q$
$g:A\to C$ by	$g(a)=p$	$g(b)=q$	$g(c)=p$
$h:B\to C$ by	$h(a)=p$	$h(b)=q$	$h(c)=r$	$h(d)=q$

1. Draw an arrow diagram for each function.

2. Determine the inverse of each function as a set of ordered pairs.

3. 1. Is $f^{-1}$ a function from $C$ to $A$? Explain.

   2. Is $g^{-1}$ a function from $C$ to $A$? Explain.

   3. Is $h^{-1}$ a function from $C$ to $B$? Explain.

   4. Draw an arrow diagram for each inverse from Part (3) that is a function. Use your existing arrow diagram from Part (1) to draw this arrow diagram.

   5. Make a conjecture about what conditions on a function $F:S\to T$ will ensure that its inverse is a function from $T$ to $S$.

6.5.7 Conditions for an Inverse Function

We will now consider a general argument suggested by the explorations in Progress Check 6.24. By definition, if $f:A\to B$ is a function, then $f^{-1}$ is a subset of $B\times A$. However, $f^{-1}$ may or may not be a function from $B$ to $A$. For example, suppose that $s,t\in A$ with $s\ne t$ and $f(s)=f(t)$. This is represented in Figure 6.9.

Figure 6.9: The Inverse Is Not a Function

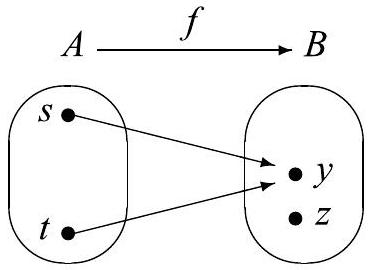
In this case, if we try to reverse the arrows, we will not get a function from $B$ to $A$. This is because $(y,s)\in f^{-1}$ and $(y,t)\in f^{-1}$ with $s\ne t$. Consequently, $f^{-1}$ is not a function. This suggests that when $f$ is not an injection, then $f^{-1}$ is not a function.

Also, if $f$ is not a surjection, then there exists a $z\in B$ such that $f(a)\ne z$ for all $a\in A$, as in the diagram in Figure 6.9. In other words, there is no ordered pair in $f$ with $z$ as the second coordinate. This means that there would be no ordered pair in $f^{-1}$ with $z$ as a first coordinate. Consequently, $f^{-1}$ cannot be a function from $B$ to $A$.

This motivates the statement in Theorem 6.25. In the proof of this theorem, we will frequently change back and forth from the input-output representation of a function and the ordered pair representation of a function. The idea is that if $G:S\to T$ is a function, then for $s\in S$ and $t\in T$,

$$G(s)=t\text{ if and only if }(s,t)\in G.$$

When we use the ordered pair representation of a function, we will also use the ordered pair representation of its inverse. In this case, we know that

$$(s,t)\in G\text{ if and only if }(t,s)\in G^{-1}.$$

Theorem 6.25. Let $A$ and $B$ be nonempty sets and let $f:A\to B$. The inverse of $f$ is a function from $B$ to $A$ if and only if $f$ is a bijection.

Proof. Let $A$ and $B$ be nonempty sets and let $f:A\to B$. We will first assume
that $f$ is a bijection and prove that $f^{-1}$ is a function from $B$ to $A$. To do this, we will show that $f^{-1}$ satisfies the two conditions of Theorem 6.22.

We first choose $b\in B$. Since the function $f$ is a surjection, there exists an $a\in A$ such that $f(a)=b$. This implies that $(a,b)\in f$ and hence that $(b,a)\in f^{-1}$. Thus, each element of $B$ is the first coordinate of an ordered pair in $f^{-1}$, and hence $f^{-1}$ satisfies the first condition of Theorem 6.22.

To prove that $f^{-1}$ satisfies the second condition of Theorem 6.22, we must show that each element of $B$ is the first coordinate of exactly one ordered pair in $f^{-1}$. So let $b\in B,a_1,a_2\in A$ and assume that

$$(b,a_1)\in f^{-1}\text{ and }(b,a_2)\in f^{-1}$$

This means that $(a_1,b)\in f$ and $(a_2,b)\in f$. We can then conclude that

$$f\left(a_1\right)=b\text{ and }f\left(a_2\right)=b$$

But this means that $f\left(a_1\right)=f\left(a_2\right)$. Since $f$ is a bijection, it is an injection, and we can conclude that $a_1=a_2$. This proves that $b$ is the first element of only one ordered pair in $f^{-1}$. Consequently, we have proved that $f^{-1}$ satisfies both conditions of Theorem 6.22 and hence that $f^{-1}$ is a function from $B$ to $A$.

We now assume that $f^{-1}$ is a function from $B$ to $A$ and prove that $f$ is a bijection. First, to prove that $f$ is an injection, we assume that $a_1,a_2\in A$ and that $f\left(a_1\right)=f\left(a_2\right)$. We wish to show that $a_1=a_2$. If we let $b=f\left(a_1\right)=f\left(a_2\right)$, we can conclude that

$$(a_1,b)\in f\text{ and }(a_2,b)\in f$$

But this means that

$$(b,a_1)\in f^{-1}\text{ and }(b,a_2)\in f^{-1}$$

Since we have assumed that $f^{-1}$ is a function, we can conclude that $a_1=a_2$. Hence, $f$ is an injection.

Now to prove that $f$ is a surjection, we choose $b\in B$ and will show that there exists an $a\in A$ such that $f(a)=b$. Since $f^{-1}$ is a function, $b$ must be the first coordinate of some ordered pair in $f^{-1}$. Consequently, there exists an $a\in A$ such that

$$(b,a)\in f^{-1}$$

Now this implies that $(a,b)\in f$ and hence that $f(a)=b$. This proves that $f$ is a surjection. Since we have also proved that $f$ is an injection, we conclude that $f$ is a bijection.

6.5.8 Inverse Function Notation

In the situation where $f:A\to B$ is a bijection and $f^{-1}$ is a function from $B$ to $A$, we can write $f^{-1}:B\to A$. In this case, we frequently say that $f$ is an invertible function, and we usually do not use the ordered pair representation for either $f$ or $f^{-1}$. Instead of writing $(a,b)\in f$, we write $f(a)=b$, and instead of writing $(b,a)\in f^{-1}$, we write $f^{-1}(b)=a$. Using the fact that $(a,b)\in f$ if and only if $(b,a)\in f^{-1}$, we can now write $f(a)=b$ if and only if $f^{-1}(b)=a$. We summarize this in Theorem 6.26.

Theorem 6.26. Let $A$ and $B$ be nonempty sets and let $f:A\to B$ be a bijection. Then $f^{-1}:B\to A$ is a function, and for every $a\in A$ and $b\in B$,

$$f(a)=b\text{ if and only if }{f}^{-1}(b)=a.$$

6.5.9 Example 6.27 (Inverse Function Notation)

For an example of the use of the notation in Theorem 6.26, let ${ℝ}^{+}=\{x\in ℝ\mid x>0\}$. Define

$$f:ℝ\to ℝ\text{ by }f(x)=x^3;\text{ and }g:ℝ\to {ℝ}^{+}\text{by }g(x)=e^x$$

Notice that ${ℝ}^{+}$is the codomain of $g$. We can then say that both $f$ and $g$ are bijections. Consequently, the inverses of these functions are also functions. In fact,

$$f^{-1}:ℝ\to ℝ\text{ by }{f}^{-1}(y)=\sqrt[3]{y};\text{ and }{g}^{-1}:{ℝ}^{+}\to ℝ\text{ by }{g}^{-1}(y)=\ln y.$$

For each function (and its inverse), we can write the result of Theorem 6.26 as follows:

Theorem 6.26	Translates to:
For $x,y\in ℝ,f(x)=y$ if and only if $f^{-1}(y)=x$.	For $x,y\in ℝ,x^3=y$ if and only if $\sqrt[3]{y}=x$.
For $x\in ℝ,y\in {ℝ}^{+},g(x)=y$ if and only if $g^{-1}(y)=x$.	For $x\in ℝ,y\in {ℝ}^{+},e^x=y$ if and only if $\ln y=x$.

6.5.10 Theorems about Inverse Functions

The next two results in this section are two important theorems about inverse functions. The first is actually a corollary of Theorem 6.26.

Corollary 6.28. Let $A$ and $B$ be nonempty sets and let $f:A\to B$ be a bijection. Then

1. For every $x$ in $A,\left(f^{-1}\circ f\right)(x)=x$.

2. For every $y$ in $B,\left(f\circ f^{-1}\right)(y)=y$.

Proof. Let $A$ and $B$ be nonempty sets and assume that $f:A\to B$ is a bijection. So let $x\in A$ and let $f(x)=y$. By Theorem 6.26, we can conclude that $f^{-1}(y)=x$. Therefore,

$\left(f^{-1}\circ f\right)(x)$ $=f^{-1}(f(x))$

$=f^{-1}(y)$

$=x$

Hence, for each $x\in A,\left(f^{-1}\circ f\right)(x)=x$.
The proof that for each $y$ in $B,\left(f\circ f^{-1}\right)(y)=y$ is Exercise (4).

6.5.11 Example 6.27 (continued)

For the cubing function and the cube root function, we have seen that

$$\text{ For }x,y\in ℝ,x^3=y\text{ if and only if }\sqrt[3]{y}=x$$

Notice that

• If we substitute $x^3=y$ into the equation $\sqrt[3]{y}=x$, we obtain $\sqrt[3]{x^3}=x$.

• If we substitute $\sqrt[3]{y}=x$ into the equation $x^3=y$, we obtain ${(\sqrt[3]{y})}^3=y$.

This is an illustration of Corollary 6.28. We can see this by using $f:ℝ\to ℝ$ defined by $f(x)=x^3$ and $f^{-1}:ℝ\to ℝ$ defined by $f^{-1}(y)=\sqrt[3]{y}$. Then $f^{-1}\circ f:ℝ\to ℝ$ and $f^{-1}\circ f=I_{ℝ}$. So for each $x\in ℝ$,

$$\begin{array}{c}\hfill \left(f^{-1}\circ f\right)(x)=x\\ \hfill f^{-1}(f(x))=x\\ \hfill f^{-1}\left(x^3\right)=x\\ \hfill \sqrt[3]{x^3}=x\end{array}$$

Similarly, the equation ${(\sqrt[3]{y})}^3=y$ for each $y\in ℝ$ can be obtained from the fact that for each $y\in ℝ,\left(f\circ f^{-1}\right)(y)=y$.

We will now consider the case where $f:A\to B$ and $g:B\to C$ are both bijections. In this case, $f^{-1}:B\to A$ and $g^{-1}:C\to B$. Figure 6.10 can be used to illustrate this situation.

Figure 6.10: Composition of Two Bijections

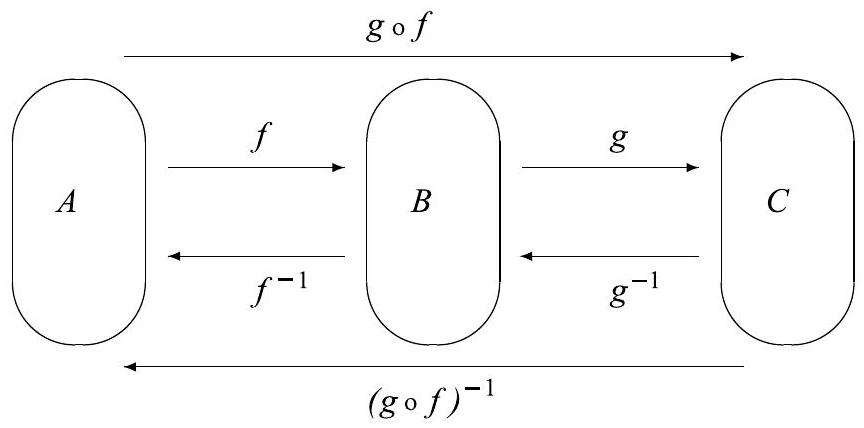
By Theorem 6.20, $g\circ f:A\to C$ is also a bijection. Hence, by Theorem 6.25, ${(g\circ f)}^{-1}$ is a function and, in fact, ${(g\circ f)}^{-1}:C\to A$. Notice that we can also form the composition of $g^{-1}$ followed by $f^{-1}$ to get $f^{-1}\circ g^{-1}:C\to A$. Figure 6.10 helps illustrate the result of the next theorem.

Theorem 6.29. Let $f:A\to B$ and $g:B\to C$ be bijections. Then $g\circ f$ is a bijection and ${(g\circ f)}^{-1}=f^{-1}\circ g^{-1}$.

Proof. Let $f:A\to B$ and $g:B\to C$ be bijections. Then $f^{-1}:B\to A$ and $g^{-1}:C\to B$. Hence, $f^{-1}\circ g^{-1}:C\to A$. Also, by Theorem 6.20, $g\circ f:A\to C$ is a bijection, and hence ${(g\circ f)}^{-1}:C\to A$. We will now prove that for each $z\in C,{(g\circ f)}^{-1}(z)=\left(f^{-1}\circ g^{-1}\right)(z)$.

Let $z\in C$. Since the function $g$ is a surjection, there exists a $y\in B$ such that

$$g(y)=z.$$ (1)

Also, since $f$ is a surjection, there exists an $x\in A$ such that

$$f(x)=y.$$ (2)

Now these two equations can be written in terms of the respective inverse functions as

$g^{-1}(z)$ $=y;\text{ and}$ (3)

$f^{-1}(y)$ $=x.$ (4)

Using equations (3) and (4), we see that

$\left(f^{-1}\circ g^{-1}\right)(z)$ $=f^{-1}\left(g^{-1}(z)\right)$

$=f^{-1}(y)$

$=x$ (5)

Using equations (1) and (2) again, we see that $(g\circ f)(x)=z$. However, in terms of the inverse function, this means that

$${(g\circ f)}^{-1}(z)=x$$ (6)

Comparing equations (5) and (6), we have shown that for all $z\in C$, ${(g\circ f)}^{-1}(z)=\left(f^{-1}\circ g^{-1}\right)(z)$. This proves that ${(g\circ f)}^{-1}=f^{-1}\circ g^{-1}$.

6.5.12 Exercises 6.5

1. Let $A=\{1,2,3\}$ and $B=\{a,b,c\}$.

   1. Construct an example of a function $f:A\to B$ that is not a bijection. Write the inverse of this function as a set of ordered pairs. Is the inverse of $f$ a function? Explain. If so, draw an arrow diagram for $f$ and $f^{-1}$.

   2. Construct an example of a function $g:A\to B$ that is a bijection. Write the inverse of this function as a set of ordered pairs. Is the inverse of $g$ a function? Explain. If so, draw an arrow diagram for $g$ and $g^{-1}$.

2. Let $S=\{a,b,c,d\}$. Define $f:S\to S$ by defining $f$ to be the following set of ordered pairs.

   $$f=\{(a,c),(b,b),(c,d),(d,a)\}$$

   1. Draw an arrow diagram to represent the function $f$. Is the function $f$ a bijection?

   2. $(\star )$ Write the inverse of $f$ as a set of ordered pairs. Is $f^{-1}$ a function? Explain.

   3. Draw an arrow diagram for $f^{-1}$ using the arrow diagram from Exercise (2a).

   4. $(\star )$ Compute $\left(f^{-1}\circ f\right)(x)$ and $\left(f\circ f^{-1}\right)(x)$ for each $x$ in $S$. What theorem does this illustrate?

3. $(\star )$ Inverse functions can be used to help solve certain equations. The idea is to use an inverse function to undo the function.

   1. Since the cube root function and the cubing function are inverses of each other, we can often use the cube root function to help solve an equation involving a cube. For example, the main step in solving the equation

      $${(2t-1)}^3=20$$

      is to take the cube root of each side of the equation. This gives

      $$\begin{array}{c}\hfill \sqrt[3]{{(2t-1)}^3}=\sqrt[3]{20}\\ \hfill 2t-1=\sqrt[3]{20}\end{array}$$

      Explain how this step in solving the equation is a use of Corollary 6.28.

   2. A main step in solving the equation $e^{2t-1}=20$ is to take the natural logarithm of both sides of this equation. Explain how this step is a use of Corollary 6.28, and then solve the resulting equation to obtain a solution for $t$ in terms of the natural logarithm function.

   3. How are the methods of solving the equations in Exercise (3a) and Exercise (3b) similar?

4. $(\star )$ Prove Part (2) of Corollary 6.28. Let $A$ and $B$ be nonempty sets and let $f:A\to B$ be a bijection. Then for every $y$ in $B,\left(f\circ f^{-1}\right)(y)=y$.

5. In Progress Check 6.6, we defined the identity function on a set. The identity function on the set $𝑻$, denoted by $I_T$, is the function $I_T:T\to T$ defined by $I_T(t)=t$ for every $t$ in $T$. Explain how Corollary 6.28 can be stated using the concept of equality of functions and the identity functions on the sets $A$ and $B$.

6. Let $f:A\to B$ and $g:B\to A$. Let $I_A$ and $I_B$ be the identity functions on the sets $A$ and $B$, respectively. Prove each of the following:

   1. $(\star )$ If $g\circ f=I_A$, then $f$ is an injection.

   2. $(\star )$ If $f\circ g=I_B$, then $f$ is a surjection.

   3. If $g\circ f=I_A$ and $f\circ g=I_B$, then $f$ and $g$ are bijections and $g=f^{-1}$.

7. $(\star )$

   1. Define $f:ℝ\to ℝ$ by $f(x)=e^{-x^2}$. Is the inverse of $f$ a function? Justify your conclusion.

   2. Let ${ℝ}^{\ast }=\{x\in ℝ\mid x\ge 0\}$. Define $g:{ℝ}^{\ast }\to (0,1]$ by $g(x)=e^{-x^2}$. Is the inverse of $g$ a function? Justify your conclusion.

8. 1. Let $f:ℝ\to ℝ$ be defined by $f(x)=x^2$. Explain why the inverse of $f$ is not a function.

   2. Let ${ℝ}^{\ast }=\{t\in ℝ\mid t\ge 0\}$. Define $g:{ℝ}^{\ast }\to {ℝ}^{\ast }$ by $g(x)=x^2$. Explain why this squaring function (with a restricted domain and codomain) is a bijection.

   3. Explain how to define the square root function as the inverse of the function in Exercise (8b).

   4. True or false: ${(\sqrt{x})}^2=x$ for all $x\in ℝ$ such that $x\ge 0$.

   5. True or false: $\sqrt{x^2}=x$ for all $x\in ℝ$.

9. Prove the following:

   If $f:A\to B$ is a bijection, then $f^{-1}:B\to A$ is also a bijection.

10. For each natural number $k$, let $A_k$ be a set, and for each natural number $n$, let $f_n:A_n\to A_{n+1}$.

    For example, $f_1:A_1\to A_2,f_2:A_2\to A_3,f_3:A_3\to A_4$, and so on.
    Use mathematical induction to prove that for each natural number $n$ with $n\ge 2$, if $f_1,f_2,\mathrm{\dots },f_n$ are all bijections, then $f_n\circ f_{n-1}\circ \mathrm{\cdots }\circ f_2\circ f_1$ is a bijection and

    $${\left(f_n\circ f_{n-1}\circ \mathrm{\cdots }\circ f_2\circ f_1\right)}^{-1}=f_1^{-1}\circ f_2^{-1}\circ \mathrm{\cdots }\circ f_{n-1}^{-1}\circ f_n^{-1}$$

    Note: This is an extension of Theorem 6.29. In fact, Theorem 6.29 is the basis step of this proof for $n=2$.

11. 1. Define $f:ℝ\to ℝ$ by $f(x)=x^2-4$ for all $x\in ℝ$. Explain why the inverse of the function $f$ is not a function.

    2. Let ${ℝ}^{\ast }=\{x\in ℝ\mid x\ge 0\}$ and let $T=\{y\in ℝ\mid y\ge -4\}$. Define $F:{ℝ}^{\ast }\to T$ by $F(x)=x^2-4$ for all $x\in {ℝ}^{\ast }$. Explain why the inverse of the function $F$ is a function and find a formula for $F^{-1}(y)$, where $y\in T$.

12. Let $R_5=\{0,1,2,3,4\}$.

    1. Define $f:R_5\to R_5$ by $f(x)=x^2+4(mod5)$ for all $x\in R_5$. Write the inverse of $f$ as a set of ordered pairs and explain why $f^{-1}$ is not a function.

    2. Define $g:R_5\to R_5$ by $g(x)=x^3+4(mod5)$ for all $x\in R_5$. Write the inverse of $g$ as a set of ordered pairs and explain why $g^{-1}$ is a function.

    3. Is it possible to write a formula for $g^{-1}(y)$, where $y\in R_5$? The answer to this question depends on whether or not it is possible to define a cube root of elements of $R_5$. Recall that for a real number $x$, we define the cube root of $x$ to be the real number $y$ such that $y^3=x$. That is,

       $$y=\sqrt[3]{x}\text{ if and only if }{y}^3=x$$

       Using this idea, is it possible to define the cube root of each number in $R_5$? If so, what are $\sqrt[3]{0},\sqrt[3]{1},\sqrt[3]{2},\sqrt[3]{3}$, and $\sqrt[3]{4}$?

    4. Now answer the question posed at the beginning of Part (c). If possible, determine a formula for $g^{-1}(y)$ where $g^{-1}:R_5\to R_5$.

6.5.13 Explorations and Activities

1. Constructing an Inverse Function. If $f:A\to B$ is a bijection, then we know that its inverse is a function. If we are given a formula for the function $f$, it may be desirable to determine a formula for the function $f^{-1}$. This can sometimes be done, while at other times it is very difficult or even impossible.

   Let $f:ℝ\to ℝ$ be defined by $f(x)=2x^3-7$. A graph of this function would suggest that this function is a bijection.

   1. Prove that the function $f$ is an injection and a surjection.

      Let $y\in ℝ$. One way to prove that $f$ is a surjection is to set $y=f(x)$ and solve for $x$. If this can be done, then we would know that there exists an $x\in ℝ$ such that $f(x)=y$. For the function $f$, we are using $x$ for the
      input and $y$ for the output. By solving for $x$ in terms of $y$, we are attempting to write a formula where $y$ is the input and $x$ is the output. This formula represents the inverse function.

   2. Solve the equation $y=2x^3-7$ for $x$. Use this to write a formula for $f^{-1}(y)$, where $f^{-1}:ℝ\to ℝ$.

   3. Use the result of Part (13b) to verify that for each $x\in ℝ,f^{-1}(f(x))=x$ and for each $y\in ℝ,f\left(f^{-1}(y)\right)=y$.

      Now let ${ℝ}^{+}=\{y\in ℝ\mid y>0\}$. Define $g:ℝ\to {ℝ}^{+}$by $g(x)=e^{2x-1}$.

   4. Set $y=e^{2x-1}$ and solve for $x$ in terms of $y$.

   5. Use your work in Exercise (13d) to define a function $h:{ℝ}^{+}\to ℝ$.

   6. For each $x\in ℝ$, determine $(h\circ g)(x)$ and for each $y\in {ℝ}^{+}$, determine $(g\circ h)(y)$.

   7. Use Exercise (6) to explain why $h=g^{-1}$.

2. The Inverse Sine Function. We have seen that in order to obtain an inverse function, it is sometimes necessary to restrict the domain (or the codomain) of a function.

   1. Let $f:ℝ\to ℝ$ be defined by $f(x)=\sin x$. Explain why the inverse of the function $f$ is not a function. (A graph may be helpful.)

      Notice that if we use the ordered pair representation, then the sine function can be represented as

      $$f=\{(x,y)\in ℝ\times ℝ\mid y=\sin x\}.$$

      If we denote the inverse of the sine function by ${\sin }^{-1}$, then

      $$f^{-1}=\{(y,x)\in ℝ\times ℝ\mid y=\sin x\}.$$

      Part (14a) proves that $f^{-1}$ is not a function. However, in previous mathematics courses, we frequently used the "inverse sine function." This is not really the inverse of the sine function as defined in Part (14a) but, rather, it is the inverse of the sine function restricted to the domain $[-\frac{\pi }{2},\frac{\pi }{2}]$.

   2. Explain why the function $F:[-\frac{\pi }{2},\frac{\pi }{2}]\to [-1,1]$ defined by $F(x)=\sin x$ is a bijection.

      The inverse of the function in Part (14b) is itself a function and is called the inverse sine function (or sometimes the arcsine function).

   3. What is the domain of the inverse sine function? What are the range and codomain of the inverse sine function?

      Let us now use $F(x)=\mathrm{Sin}(x)$ to represent the restricted sine function in Part (14b). Therefore, $F^{-1}(x)={\mathrm{Sin}}^{-1}(x)$ can be used to represent the inverse sine function. Observe that

      $$F:[-\frac{\pi }{2},\frac{\pi }{2}]\to [-1,1]\text{ and }{F}^{-1}:[-1,1]\to [-\frac{\pi }{2},\frac{\pi }{2}]$$

   4. Using this notation, explain why

      ${\mathrm{Sin}}^{-1}y=x\text{ if and only if }\left[y=\sin x\text{ and }-{\displaystyle \frac{\pi }{2}}\le x\le {\displaystyle \frac{\pi }{2}}\right]$

      $\mathrm{Sin}\left({\mathrm{Sin}}^{-1}(y)\right)=y\text{ for all }y\in [-1,1];\text{ and}$

      $\mathrm{Sin}{}_{}{}^{-1}(\mathrm{Sin}(x))=x\text{ for all }x\in [-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}]$