6 Functions

6.6 Functions Acting on Sets

6.6.1 Beginning Activity 1 (Functions and Sets)

Let $S=\{a,b,c,d\}$ and $T=\{s,t,u\}$. Define $f:S\to T$ by

$$f(a)=sf(b)=tf(c)=tf(d)=s$$

1. Let $A=\{a,c\}$ and $B=\{a,d\}$. Notice that $A$ and $B$ are subsets of $S$. Use the roster method to specify the elements of the following two subsets of $T$ :

   1. $\{f(x)\mid x\in A\}$

   2. $\{f(x)\mid x\in B\}$

2. Let $C=\{s,t\}$ and $D=\{s,u\}$. Notice that $C$ and $D$ are subsets of $T$. Use the roster method to specify the elements of the following two subsets of $S$ :

   1. $\{x\in S\mid f(x)\in C\}$

   2. $\{x\in S\mid f(x)\in D\}$

Now let $g:ℝ\to ℝ$ be defined by $g(x)=x^2$, for each $x\in ℝ$.

1. Let $A=\{1,2,3,-1\}$. Use the roster method to specify the elements of the set $\{g(x)\mid x\in A\}$.

2. Use the roster method to specify the elements of each of the following sets:

   1. $\{x\in ℝ\mid g(x)=1\}$

   2. $\{x\in ℝ\mid g(x)=9\}$

   3. $\{x\in ℝ\mid g(x)=15\}$

   4. $\{x\in ℝ\mid g(x)=-1\}$

3. Let $B=\{1,9,15,-1\}$. Use the roster method to specify the elements of the set $\{x\in ℝ\mid g(x)\in B\}$.

6.6.2 Beginning Activity 2 (Functions and Intervals)

Let $g:ℝ\to ℝ$ be defined by $g(x)=x^2$, for each $x\in ℝ$.

1. We will first determine where $g$ maps the closed interval $[1,2]$. (Recall that $[1,2]=\{x\in ℝ\mid 1\le x\le 2\}$.) That is, we will describe, in simpler terms, the set $\{g(x)\mid x\in [1,2]\}$. This is the set of all images of the real numbers in the closed interval $[1,2]$.

   1. Draw a graph of the function $g$ using $-3\le x\le 3$.

   2. On the graph, draw the vertical lines $x=1$ and $x=2$ from the $x$-axis to the graph. Label the points $P(1,f(1))$ and $Q(2,f(2))$ on the graph.

   3. Now draw horizontal lines from the points $P$ and $Q$ to the $y$-axis. Use this information from the graph to describe the set $\{g(x)\mid x\in [1,2]\}$ in simpler terms. Use interval notation or set builder notation.

2. We will now determine all real numbers that $g$ maps into the closed interval $[1,4]$. That is, we will describe the set $\{x\in ℝ\mid g(x)\in [1,4]\}$ in simpler terms. This is the set of all preimages of the real numbers in the closed interval $[1,4]$.

   1. Draw a graph of the function $g$ using $-3\le x\le 3$.

   2. On the graph, draw the horizontal lines $y=1$ and $y=4$ from the $y$-axis to the graph. Label all points where these two lines intersect the graph.

   3. Now draw vertical lines from the points in Part (2) to the $x$-axis, and then use the resulting information to describe the set $\{x\in ℝ\mid g(x)\in [1,4]\}$ in simpler terms. (You will need to describe this set as a union of two intervals. Use interval notation or set builder notation.)

6.6.3 Functions Acting on Sets

In our study of functions, we have focused on how a function "maps" individual elements of its domain to the codomain. We also studied the preimage of an individual element in its codomain. For example, if $f:ℝ\to ℝ$ is defined by $f(x)=x^2$, for each $x\in ℝ$, then

• $f(2)=4$. We say that $f$ maps 2 to 4 or that 4 is the image of 2 under the function $f$.

• Since $f(x)=4$ implies that $x=2$ or $x=-2$, we say that the preimages of 4 are 2 and -2 or that the set of preimages of 4 is $\{-2,2\}$.

For a function $f:S\to T$, the next step is to consider subsets of $S$ or $T$ and what corresponds to them in the other set. We did this in the beginning activities. We will give some definitions and then revisit the examples in the beginning activities in light of these definitions. We will first consider the situation where $A$ is a subset of $S$ and consider the set of outputs whose inputs are from $A$. This will be a subset of $T$.

Definition. Let $f:S\to T$. If $A\subseteq S$, then the image of $𝑨$ under $𝒇$ is the set $f(A)$, where

$$f(A)=\{f(x)\mid x\in A\}$$

If there is no confusion as to which function is being used, we call $f(A)$ the image of $𝑨$.

We now consider the situation in which $C$ is a subset of $T$ and consider the subset of $A$ consisting of all elements of $T$ whose outputs are in $C$.

Definition. Let $f:S\to T$. If $C\subseteq T$, then the preimage of $𝑪$ under $𝒇$ is the set $f^{-1}(C)$, where

$$f^{-1}(C)=\{x\in S\mid f(x)\in C\}$$

If there is no confusion as to which function is being used, we call $f^{-1}(C)$ the preimage of $𝑪$. The preimage of the set $C$ under $f$ is also called the inverse image of $𝑪$ under $𝒇$.

Notice that the set $f^{-1}(C)$ is defined whether or not $f^{-1}$ is a function.

6.6.4 Progress Check 6.30 (Beginning Activity 1 Revisited)

Let $S=\{a,b,c,d\}$ and $T=\{s,t,u\}$. Define $f:S\to T$ by

$$f(a)=sf(b)=tf(c)=tf(d)=s$$

Let $A=\{a,c\},B=\{a,d\},C=\{s,t\},$ and $D=\{s,u\}$.
Use your work in Beginning Activity 1 to determine each of the following sets:

1. $f(A)$

2. $f(B)$

3. $f^{-1}(C)$

4. $f^{-1}(D)$

6.6.5 Example 6.31 (Images and Preimages of Sets)

Let $f:ℝ\to ℝ$ be defined by $f(x)=x^2$, for each $x\in ℝ$. The following results are based on the examples in Beginning Activity 1 and Beginning Activity 2.

• Let $A=\{1,2,3,-1\}$. Then $f(A)=\{1,4,9\}$.

• Let $B=\{1,9,15,-1\}$. Then $f^{-1}(B)=\{-\sqrt{15},-3,-1,1,3,\sqrt{15}\}$.

The graphs from Beginning Activity 2 illustrate the following results:

• If $T$ is the closed interval [1,2], then the image of the set $T$ is

$f(T)$ $=\{f(x)\mid x\in [1,2]\}$

$=[1,4].$

• If $C$ is the closed interval $[1,4]$, then the preimage of the set $C$ is

$$f^{-1}(C)=\{x\in ℝ\mid f(x)\in [1,4]\}=[-2,-1]\cup [1,2].$$

6.6.6 Set Operations and Functions Acting on Sets

We will now consider the following situation: Let $S$ and $T$ be sets and let $f$ be a function from $S$ to $T$. Also, let $A$ and $B$ be subsets of $S$ and let $C$ and $D$ be subsets of $T$. In the remainder of this section, we will consider the following situations and answer the questions posed in each case.

• The set $A\cap B$ is a subset of $S$ and so $f(A\cap B)$ is a subset of $T$. In addition, $f(A)$ and $f(B)$ are subsets of $T$. Hence, $f(A)\cap f(B)$ is a subset of $T$.

Is there any relationship between $f(A\cap B)$ and $f(A)\cap f(B)$ ?

• The set $A\cup B$ is a subset of $S$ and so $f(A\cup B)$ is a subset of $T$. In addition, $f(A)$ and $f(B)$ are subsets of $T$. Hence, $f(A)\cup f(B)$ is a subset of $T$.
  Is there any relationship between $f(A\cup B)$ and $f(A)\cup f(B)$ ?

• The set $C\cap D$ is a subset of $T$ and so $f^{-1}(C\cap D)$ is a subset of $S$. In addition, $f^{-1}(C)$ and $f^{-1}(D)$ are subsets of $S$. Hence, $f^{-1}(C)\cap f^{-1}(D)$ is a subset of $S$.

Is there any relationship between the sets $f^{-1}(C\cap D)$ and $f^{-1}(C)\cap f^{-1}(D)$ ?

• The set $C\cup D$ is a subset of $T$ and so $f^{-1}(C\cup D)$ is a subset of $S$. In addition, $f^{-1}(C)$ and $f^{-1}(D)$ are subsets of $S$. Hence, $f^{-1}(C)\cup f^{-1}(D)$ is a subset of $S$.

Is there any relationship between the sets $f^{-1}(C\cup D)$ and $f^{-1}(C)\cup f^{-1}(D)$ ?

These and other questions will be explored in the next progress check.

6.6.7 Progress Check 6.32 (Set Operations and Functions Acting on Sets)

In Section 6.2, we introduced functions involving congruences. For example, if we let

$$R_8=\{0,1,2,3,4,5,6,7\},$$

then we can define $f:R_8\to R_8$ by $f(x)=r$, where $\left(x^2+2\right)\equiv r(mod8)$ and $r\in R_8$. Moreover, we shortened this notation to

$$f(x)=\left(x^2+2\right)(mod8)$$

We will use the following subsets of $R_8$ :

$$A=\{1,2,4\}B=\{3,4,6\}C=\{1,2,3\}D=\{3,4,5\}.$$

1. Verify that $f(0)=2,f(1)=3,f(2)=6$, and $f(3)=3$. Then determine $f(4),f(5),f(6)$, and $f(7)$.

2. Determine $f(A),f(B),f^{-1}(C)$, and $f^{-1}(D)$.

3. For each of the following, determine the two subsets of $R_8$ and then determine if there is a relationship between the two sets. For example, $A\cap B=\{4\}$ and since $f(4)=2$, we see that $f(A\cap B)=\{2\}$.

   1. $f(A\cap B)$ and $f(A)\cap f(B)$

   2. $f(A\cup B)$ and $f(A)\cup f(B)$

   3. $f^{-1}(C\cap D)$ and $f^{-1}(C)\cap f^{-1}(D)$

   4. $f^{-1}(C\cup D)$ and $f^{-1}(C)\cup f^{-1}(D)$

4. Notice that $f(A)$ is a subset of the codomain, $R_8$. Consequently, $f^{-1}(f(A))$ is a subset of the domain, $R_8$. Is there any relation between $A$ and $f^{-1}(f(A))$ in this case?

5. Notice that $f^{-1}(C)$ is a subset of the domain, $R_8$. Consequently, $f\left(f^{-1}(C)\right)$ is a subset of the codomain, $R_8$. Is there any relation between $C$ and $f\left(f^{-1}(C)\right)$ in this case?

6.6.8 Example 6.33 (Set Operations and Functions Acting on Sets)

Define $f:ℝ\to ℝ$ by $f(x)=x^2+2$ for all $x\in ℝ$. It will be helpful to use the graph shown in Figure 6.11.

Figure 6.11: Graph for Example 6.33

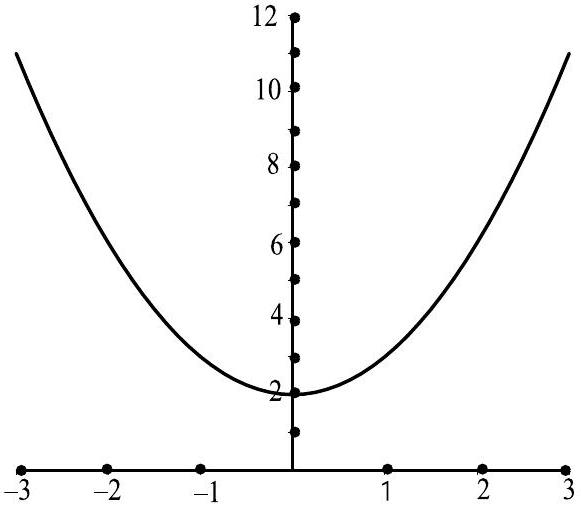
We will use the following closed intervals:

$$A=[0,3]B=[-2,1]C=[2,6]D=[0,3].$$

1. Verify that $f(A)=[2,11],f(B)=[2,6],f^{-1}(C)=[-2,2]$, and that $f^{-1}(D)=[-1,1]$.

2. 1. Explain why $f(A\cap B)=[2,3]$ and $f(A)\cap f(B)=[2,6]$. So in this case, $f(A\cap B)\subseteq f(A)\cap f(B)$.

   2. Explain why $f(A\cup B)=[2,11]$ and $f(A)\cup f(B)=[2,11]$. So in this case, $f(A\cup B)=f(A)\cup f(B)$.

   3. Explain why $f^{-1}(C\cap D)=[-1,1]$ and $f^{-1}(C)\cap f^{-1}(D)=[-1,1]$. So in this case, $f^{-1}(C\cap D)=f^{-1}(C)\cap f^{-1}(D)$.

   4. Explain why $f^{-1}(C\cup D)=[-2,2]$ and $f^{-1}(C)\cup f^{-1}(D)=[-2,2]$. So in this case, $f^{-1}(C\cup D)=f^{-1}(C)\cup f^{-1}(D)$.

3. Recall that $A=[0,3]$. Notice $f(A)=[2,11]$ is a subset of the codomain, $ℝ$. Explain why $f^{-1}(f(A))=[-3,3]$. Since $f^{-1}(f(A))$ is a subset of the domain, $ℝ$, we see that in this case, $A\subseteq f^{-1}(f(A))$.

4. Recall that $C=[2,6]$. Notice that $f^{-1}(C)=[-2,2]$ is a subset of the domain, $ℝ$. Explain why $f\left(f^{-1}(C)\right)=[2,6]$. Since $f\left(f^{-1}(C)\right)$ is a subset of the codomain, $ℝ$, we see that in this case $f\left(f^{-1}(C)\right)=C$.

The examples in Progress Check 6.32 and Example 6.33 were meant to illustrate general results about how functions act on sets. In particular, we investigated how the action of a function on sets interacts with the set operations of intersection and union. We will now state the theorems that these examples were meant to illustrate. Some of the proofs will be left as exercises.

Theorem 6.34. Let $f:S\to T$ be a function and let $A$ and $B$ be subsets of $S$. Then

1. $f(A\cap B)\subseteq f(A)\cap f(B)$

2. $f(A\cup B)=f(A)\cup f(B)$

Proof. We will prove Part (1). The proof of Part (2) is Exercise (5).
Assume that $f:S\to T$ is a function and let $A$ and $B$ be subsets of $S$. We will prove that $f(A\cap B)\subseteq f(A)\cap f(B)$ by proving that for all $y\in T$, if $y\in f(A\cap B)$, then $y\in f(A)\cap f(B)$.

We assume that $y\in f(A\cap B)$. This means that there exists an $x\in A\cap B$ such that $f(x)=y$. Since $x\in A\cap B$, we conclude that $x\in A$ and $x\in B$.

• Since $x\in A$ and $f(x)=y$, we conclude that $y\in f(A)$.

• Since $x\in B$ and $f(x)=y$, we conclude that $y\in f(B)$.

Since $y\in f(A)$ and $y\in f(B),y\in f(A)\cap f(B)$. This proves that if $y\in f(A\cap B)$, then $y\in f(A)\cap f(B)$. Hence $f(A\cap B)\subseteq f(A)\cap f(B)$.

Theorem 6.35. Let $f:S\to T$ be a function and let $C$ and $D$ be subsets of $T$. Then

1. $f^{-1}(C\cap D)=f^{-1}(C)\cap f^{-1}(D)$

2. $f^{-1}(C\cup D)=f^{-1}(C)\cup f^{-1}(D)$

Proof. We will prove Part (2). The proof of Part (1) is Exercise (6).
Assume that $f:S\to T$ is a function and that $C$ and $D$ are subsets of $T$. We will prove that $f^{-1}(C\cup D)=f^{-1}(C)\cup f^{-1}(D)$ by proving that each set is a subset of the other.

We start by letting $x$ be an element of $f^{-1}(C\cup D)$. This means that $f(x)$ is an element of $C\cup D$. Hence,

$$f(x)\in C\text{ or }f(x)\in D$$

In the case where $f(x)\in C$, we conclude that $x\in f^{-1}(C)$, and hence that $x\in f^{-1}(C)\cup f^{-1}(D)$. In the case where $f(x)\in D$, we see that $x\in f^{-1}(D)$, and hence that $x\in f^{-1}(C)\cup f^{-1}(D)$. So in both cases, $x\in f^{-1}(C)\cup f^{-1}(D)$, and we have proved that $f^{-1}(C\cup D)\subseteq f^{-1}(C)\cup f^{-1}(D)$.

We now let $t\in f^{-1}(C)\cup f^{-1}(D)$. This means that

$$t\in f^{-1}(C)\text{ or }t\in f^{-1}(D)$$

• In the case where $t\in f^{-1}(C)$, we conclude that $f(t)\in C$ and hence that $f(t)\in C\cup D$. This means that $t\in f^{-1}(C\cup D)$.

• Similarly, when $t\in f^{-1}(D)$, it follows that $f(t)\in D$ and hence that $f(t)\in C\cup D$. This means that $t\in f^{-1}(C\cup D)$.

These two cases prove that if $t\in f^{-1}(C)\cup f^{-1}(D)$, then $t\in f^{-1}(C\cup D)$. Therefore, $f^{-1}(C)\cup f^{-1}(D)\subseteq f^{-1}(C\cup D)$.

Since we have now proved that each of the two sets is a subset of the other set, we can conclude that $f^{-1}(C\cup D)=f^{-1}(C)\cup f^{-1}(D)$.

Theorem 6.36. Let $f:S\to T$ be a function and let $A$ be a subset of $S$ and let $C$ be a subset of $T$. Then

1. $A\subseteq f^{-1}(f(A))$

2. $f\left(f^{-1}(C)\right)\subseteq C$

Proof. We will prove Part (1). The proof of Part (2) is Exercise (7).
To prove Part (1), we will prove that for all $a\in S$, if $a\in A$, then $a\in f^{-1}(f(A))$. So let $a\in A$. Then, by definition, $f(a)\in f(A)$. We know that $f(A)\subseteq T$, and so $f^{-1}(f(A))\subseteq S$. Notice that

$$f^{-1}(f(A))=\{x\in S\mid f(x)\in f(A)\}$$

Since $f(a)\in f(A)$, we use this to conclude that $a\in f^{-1}(f(A))$. This proves that if $a\in A$, then $a\in f^{-1}(f(A))$, and hence that $A\subseteq f^{-1}(f(A))$.

6.6.9 Exercises 6.6

1. Let $f:S\to T$, let $A$ and $B$ be subsets of $S$, and let $C$ and $D$ be subsets of $T$. For $x\in S$ and $y\in T$, carefully explain what it means to say that

   1. $(\star )$ $y\in f(A\cap B)$

   2. $y\in f(A\cup B)$

   3. $y\in f(A)\cap f(B)$

   4. $(\star )$ $y\in f(A)\cup f(B)$

   5. $x\in f^{-1}(C\cap D)$

   6. $(\star )$ $x\in f^{-1}(C\cup D)$

   7. $x\in f^{-1}(C)\cap f^{-1}(D)$

   8. $(\star )$ $x\in f^{-1}(C)\cup f^{-1}(D)$

2. Let $f:ℝ\to ℝ$ by $f(x)=-2x+1$. Let
   $A=[2,5]$
   $B=[-1,3]$
   $C=[-2,3]$
   $D=[1,4]$.

   Find each of the following:

   1. $f(A)$

   2. $(\star )$ $f^{-1}(f(A))$

   3. $f^{-1}(C)$

   4. $(\star )$ $f\left(f^{-1}(C)\right)$

   5. $(\star )$ $f(A\cap B)$

   6. $(\star )$ $f(A)\cap f(B)$

   7. $f^{-1}(C\cap D)$

   8. $f^{-1}(C)\cap f^{-1}(D)$

3. Let $g:\mathbb{N}\times \mathbb{N}\to \mathbb{N}$ by $g(m,n)=2^m{3}^n$, let $A=\{1,2,3\}$, and let $C=\{1,4,6,9,12,16,18\}$. Find

   1. $(\star )$ $g(A\times A)$

   2. $(\star )$ $g^{-1}(C)$

   3. $g^{-1}(g(A\times A))$

   4. $g\left(g^{-1}(C)\right)$

4. 1. $(\star )$ Let $S=\{1,2,3,4\}$. Define $F:S\to \mathbb{N}$ by $F(x)=x^2$ for each $x\in S$. What is the range of the function $F$ and what is $F(S)$? How do these two sets compare?

      Now let $A$ and $B$ be sets and let $f:A\to B$ be an arbitrary function from $A$ to $B$.

   2. Explain why $f(A)=\mathrm{range}(f)$.

   3. Define a function $g:A\to f(A)$ by $g(x)=f(x)$ for all $x$ in $A$. Prove that the function $g$ is a surjection.

5. $(\star )$ Prove Part (2) of Theorem 6.34. Let $f:S\to T$ be a function and let $A$ and $B$ be subsets of $S$. Then $f(A\cup B)=f(A)\cup f(B)$.

6. $(\star )$ Prove Part (1) of Theorem 6.35. Let $f:S\to T$ be a function and let $C$ and $D$ be subsets of $T$. Then $f^{-1}(C\cap D)=f^{-1}(C)\cap f^{-1}(D)$.

7. Prove Part (2) of Theorem 6.36.

   Let $f:S\to T$ be a function and let $C\subseteq T$. Then $f\left(f^{-1}(C)\right)\subseteq C$.

8. Let $f:S\to T$ and let $A$ and $B$ be subsets of $S$. Prove or disprove each of the following:

   1. If $A\subseteq B$, then $f(A)\subseteq f(B)$.

   2. If $f(A)\subseteq f(B)$, then $A\subseteq B$.

9. $(\star )$ Let $f:S\to T$ and let $C$ and $D$ be subsets of $T$. Prove or disprove each of the following:

   1. If $C\subseteq D$, then $f^{-1}(C)\subseteq f^{-1}(D)$.

   2. If $f^{-1}(C)\subseteq f^{-1}(D)$, then $C\subseteq D$.

10. Prove or disprove:

    If $f:S\to T$ is a function and $A$ and $B$ are subsets of $S$, then
    $f(A)\cap f(B)\subseteq f(A\cap B)$.
    Note: Part (1) of Theorem 6.34 states that $f(A\cap B)\subseteq f(A)\cap f(B)$.

11. Let $f:S\to T$ be a function, let $A\subseteq S$, and let $C\subseteq T$.

    1. Part (1) of Theorem 6.36 states that $A\subseteq f^{-1}(f(A))$. Give an example where $f^{-1}(f(A))⊈A$.

    2. Part (2) of Theorem 6.36 states that $f\left(f^{-1}(C)\right)\subseteq C$. Give an example where $C⊈f\left(f^{-1}(C)\right)$.

12. Is the following proposition true or false? Justify your conclusion with a proof or a counterexample.
    If $f:S\to T$ is an injection and $A\subseteq S$, then $f^{-1}(f(A))=A$.

13. Is the following proposition true or false? Justify your conclusion with a proof or a counterexample.
    If $f:S\to T$ is a surjection and $C\subseteq T$, then $f\left(f^{-1}(C)\right)=C$.

14. Let $f:S\to T$. Prove that $f(A\cap B)=f(A)\cap f(B)$ for all subsets $A$ and $B$ of $S$ if and only if $f$ is an injection.

6.7 Chapter 6 Summary

6.7.1 Important Definitions

• Function, Section 6.1

• Domain of a function, Section 6.1

• Codomain of a function, Section 6.1

• Image of $x$ under $f$, Section 6.1

• preimage of $y$ under $f$, Section 6.1

• Independent variable, Section 6.1

• Dependent variable, Section 6.1

• Range of a function, Section 6.1

• Image of a function, Section 6.1

• Equal functions, Section 6.1

• Sequence, Section 6.2

• Injection, Section 6.3

• One-to-one function, Section 6.3

• Surjection, Section 6.3

• Onto function, Section 6.3

• Bijection, Section 6.3

• One-to-one and onto, Section 6.3

• Composition of $f$ and $g$, Section 6.4

• Composite function, Section 6.4

• $f$ followed by $g$, Section 6.4

• Inverse of a function, Section 6.5

• Image of a set under a function, Section 6.6

• Preimage of a set under a function, Section 6.6

6.7.2 Important Theorems and Results about Functions

• Theorem 6.20. Let $A,B$, and $C$ be nonempty sets and let $f:A\to B$ and $g:B\to C$.

1. If $f$ and $g$ are both injections, then $g\circ f$ is an injection.

2. If $f$ and $g$ are both surjections, then $g\circ f$ is a surjection.

3. If $f$ and $g$ are both bijections, then $g\circ f$ is a bijection.

• Theorem 6.21. Let $A,B$, and $C$ be nonempty sets and let $f:A\to B$ and $g:B\to C$.

1. If $g\circ f:A\to C$ is an injection, then $f:A\to B$ is an injection.

2. If $g\circ f:A\to C$ is a surjection, then $g:B\to C$ is a surjection.

• Theorem 6.22. Let $A$ and $B$ be nonempty sets and let $f$ be a subset of $A\times B$ that satisfies the following two properties:

• For every $a\in A$, there exists $b\in B$ such that $(a,b)\in f$; and

• For every $a\in A$ and every $b,c\in B$, if $(a,b)\in f$ and $(a,c)\in f$, then $b=c$.

If we use $f(a)=b$ whenever $(a,b)\in f$, then $f$ is a function from $A$ to $B$.

• Theorem 6.25. Let $A$ and $B$ be nonempty sets and let $f:A\to B$. The inverse of $f$ is a function from $B$ to $A$ if and only if $f$ is a bijection.

• Theorem 6.26. Let $A$ and $B$ be nonempty sets and let $f:A\to B$ be a bijection. Then $f^{-1}:B\to A$ is a function, and for every $a\in A$ and $b\in B$,

$$f(a)=b\text{ if and only if }{f}^{-1}(b)=a.$$

• Corollary 6.28. Let $A$ and $B$ be nonempty sets and let $f:A\to B$ be a bijection. Then

1. For every $x$ in $A,\left(f^{-1}\circ f\right)(x)=x$.

2. For every $y$ in $B,\left(f\circ f^{-1}\right)(y)=y$.

• Theorem 6.29. Let $f:A\to B$ and $g:B\to C$ be bijections. Then $g\circ f$ is a bijection and ${(g\circ f)}^{-1}=f^{-1}\circ g^{-1}$.

• Theorem 6.34. Let $f:S\to T$ be a function and let $A$ and $B$ be subsets of $S$. Then

1. $f(A\cap B)\subseteq f(A)\cap f(B)$

2. $f(A\cup B)=f(A)\cup f(B)$

• Theorem 6.35. Let $f:S\to T$ be a function and let $C$ and $D$ be subsets of $T$. Then

1. $f^{-1}(C\cap D)=f^{-1}(C)\cap f^{-1}(D)$

2. $f^{-1}(C\cup D)=f^{-1}(C)\cup f^{-1}(D)$

• •

  Theorem 6.36. Let $f:S\to T$ be a function and let $A$ be a subset of $S$ and let $C$ be a subset of $T$. Then

1. $A\subseteq f^{-1}(f(A))$

2. $f\left(f^{-1}(C)\right)\subseteq C$